摘要:∵A1E⊥平面BEP.EQ=EF=. ∴A1F=A1Q.∴△A1FP≌△A1QP,从而∠A1PF=∠A1PQ. ②由①②及MP为公共边知 △FMP≌△QMP.
网址:http://m.1010jiajiao.com/timu_id_152482[举报]
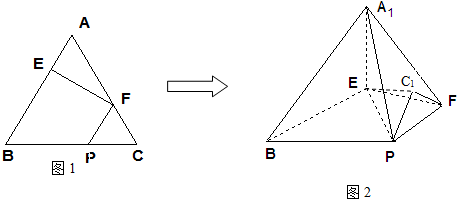
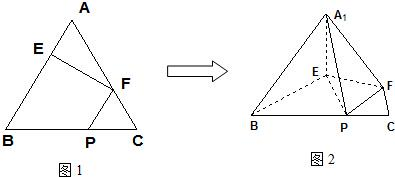
在正△ABC中,E,F,P分别是AB,AC,BC边上的点,满足
=
=
=
,将△AEF沿EF折起到△A1EF的位置,使二面角A1-EF-B成直二面角,连接A1B,A1P.
(1)求证:A1E⊥平面BEP;
(2)求直线A1E与平面A1BP所成角的大小.
 查看习题详情和答案>>
查看习题详情和答案>>
| AE |
| EB |
| CF |
| FA |
| CP |
| PB |
| 1 |
| 2 |
(1)求证:A1E⊥平面BEP;
(2)求直线A1E与平面A1BP所成角的大小.
 查看习题详情和答案>>
查看习题详情和答案>>
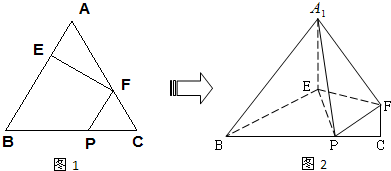
在正三角形△ABC中,E,F,P分别是AB,AC,BC边上的点,满足:AE:EB=CF:FA=CP:PB=1:2(如图1),将△AEF沿EF折成到△A1EF的位置,使二面角A1-EF-B成直二面角,连接A1B,A1P(如图2)
(1)求证:A1E⊥平面BEP;
(2)求二面角B-A1P-F的余弦值;
(3)求点F到平面A1BP的距离.
查看习题详情和答案>>

(1)求证:A1E⊥平面BEP;
(2)求二面角B-A1P-F的余弦值;
(3)求点F到平面A1BP的距离.
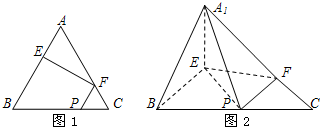 如图1,在边长为3的正三角形ABC中,E,F,P分别为AB,AC,
如图1,在边长为3的正三角形ABC中,E,F,P分别为AB,AC,BC上的点,且满足AE=FC=CP=1.将△AEF沿EF折起到△A1EF的位置,使二面角A1-EF-B成直二面角,连接A1B,A1P(如图2).
(Ⅰ)求证:A1E⊥平面BEP;
(Ⅱ)求直线A1E与平面A1BP所成角的大小.