摘要：∴△ADF是正三角形.又AE=DE=1.∴EF⊥AD----2分在图2中.A1E⊥EF.BE⊥EF.∴∠A1EB为二面角A1-EF-B的平面角由题设条件知此二面角为直二面角.∴A1E⊥BE.又BE∩EF=E.∴A1E⊥平面BEF.即A1E⊥平面BEP---.4分(II)在图2中.∵A1E不垂直于A1B.∴A1E是平面A1BP的斜线.又A1E⊥平面BEP, ∴A1E⊥BP,从而BP垂直于A1E在平面A1BP内的射影.设A1E在平面A1BP内的射影为A1Q.且A1Q交BP于点Q.则∠EA1Q就是A1E与平面A1BP所成的角.-------6分且BP⊥A1Q.在△EBP中.∵BE=BP=2.∠EBP=600. ∴△EBP是等边三角形.∴BE=EP.
网址：http://m.1010jiajiao.com/timu_id_152477[举报]
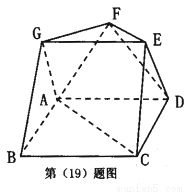
如图所示，在多面体ABCD-EFG中，四边形ABCD是边长为2的正方形，平面ABG、平面ADF、平面CDE都与平面ABCD垂直，且△ABG、△ADF、△CDE都是正三角形．
（Ⅰ）求证：AC∥EF；
（Ⅱ）求四棱锥F-ABCD的体积．
查看习题详情和答案>>
（Ⅰ）求证：AC∥EF；
（Ⅱ）求四棱锥F-ABCD的体积．
如图，在多面体ABCDEFG中，四边形ABCD是边长为2的正方形，平面ABG、平面ADF、平面CDE都与平面ABCD垂直，且ΔABG, ΔADF, ΔCDE都是正三角形.
(I)求证：AC// EF ；
(II) 求多面体ABCDEFG的体积.
查看习题详情和答案>>
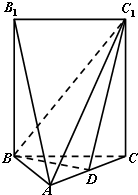如图，五面体A-BCC1B1中，AB1=4．底面ABC 是正三角形，AB=2．四边形BCC1B1是矩形，二面角A-BC-C1为直二面角．
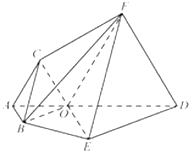平面四边形ABED中，O在线段AD上，且OA=1，OD=2，△OAB，△ODE都是正三角形．将四边形ABED沿AD翻折后，使点B落在点C位置，点E落在点F位置，且F点在平面ABED上的射影恰为线段OD的中点（即垂线段的垂足点），所得多面体ABEDFC，如图所示