摘要:由题意.得对任意R成立. --------------------8分
网址:http://m.1010jiajiao.com/timu_id_152359[举报]
设数列 的各项均为正数.若对任意的
的各项均为正数.若对任意的 ,存在
,存在 ,使得
,使得 成立,则称数列
成立,则称数列 为“Jk型”数列.
为“Jk型”数列.
(1)若数列 是“J2型”数列,且
是“J2型”数列,且 ,
, ,求
,求 ;
;
(2)若数列 既是“J3型”数列,又是“J4型”数列,证明:数列
既是“J3型”数列,又是“J4型”数列,证明:数列 是等比数列.
是等比数列.
【解析】1)中由题意,得 ,
, ,
, ,
, ,…成等比数列,且公比
,…成等比数列,且公比 ,
,
所以.
(2)中证明:由{ }是“j4型”数列,得
}是“j4型”数列,得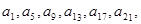 ,…成等比数列,设公比为t. 由{
,…成等比数列,设公比为t. 由{ }是“j3型”数列,得
}是“j3型”数列,得
 ,…成等比数列,设公比为
,…成等比数列,设公比为 ;
;
 ,…成等比数列,设公比为
,…成等比数列,设公比为 ;
;
 …成等比数列,设公比为
…成等比数列,设公比为 ;
;
查看习题详情和答案>>
如图,已知圆锥体 的侧面积为
的侧面积为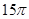 ,底面半径
,底面半径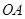 和
和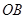 互相垂直,且
互相垂直,且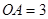 ,
, 是母线
是母线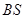 的中点.
的中点.

(1)求圆锥体的体积;
(2)异面直线 与
与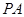 所成角的大小(结果用反三角函数表示).
所成角的大小(结果用反三角函数表示).
【解析】本试题主要考查了圆锥的体积和异面直线的所成的角的大小的求解。
第一问中,由题意, 得
得 ,故
,故
从而体积 .2中取OB中点H,联结PH,AH.
.2中取OB中点H,联结PH,AH.
由P是SB的中点知PH//SO,则 (或其补角)就是异面直线SO与PA所成角.
(或其补角)就是异面直线SO与PA所成角.
由SO 平面OAB,
平面OAB, PH
PH 平面OAB,PH
平面OAB,PH AH.在
AH.在 OAH中,由OA
OAH中,由OA OB得
OB得 ;
;
在 中,
中, ,PH=1/2SB=2,
,PH=1/2SB=2, ,
,
则 ,所以异面直线SO与P成角的大arctan
,所以异面直线SO与P成角的大arctan
解:(1)由题意, 得
得 ,
,
故 从而体积
从而体积 .
.
(2)如图2,取OB中点H,联结PH,AH.
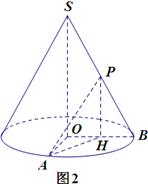
由P是SB的中点知PH//SO,则 (或其补角)就是异面直线SO与PA所成角.
(或其补角)就是异面直线SO与PA所成角.
由SO 平面OAB,
平面OAB, PH
PH 平面OAB,PH
平面OAB,PH AH.
AH.
在 OAH中,由OA
OAH中,由OA OB得
OB得 ;
;
在 中,
中, ,PH=1/2SB=2,
,PH=1/2SB=2, ,
,
则 ,所以异面直线SO与P成角的大arctan
,所以异面直线SO与P成角的大arctan
查看习题详情和答案>>
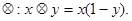 若不等式
若不等式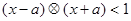 对任意实数
对任意实数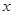 成则
成则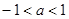 B.
B.
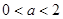
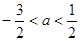 D.
D.
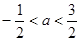
 是等差数列,其前n项和为Sn,
是等差数列,其前n项和为Sn, 是等比数列,且
是等比数列,且 ,
, .
. ,
, ,证明
,证明 (
( 的公差为d,等比数列
的公差为d,等比数列 的公比为q.
的公比为q. ,得
,得 ,
, ,
, .
. ,解得
,解得
 ,
, ,
, .
. ①
① ②
②



 ,
,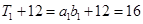 ,
, ,故等式成立.
,故等式成立. ,则当n=k+1时,有:
,则当n=k+1时,有:





 ,因此n=k+1时等式也成立
,因此n=k+1时等式也成立