摘要:17.(1)利用赋值法易得.
网址:http://m.1010jiajiao.com/timu_id_150316[举报]
观察下列问题:
已知(1-2x)2013=a0+a1x+a2x2+a3x3+…+a2013x2013,
令x=0,可得a0=1,
令x=1,可得a0+a1+a2+a3+…+a2013=(1-2•1)2013=-1,
令x=-1,可得a0-a1+a2+a3+…-a2013=(1+2•1)2013=32013,
请仿照这种“赋值法”,求出
+
+
+…+
=
查看习题详情和答案>>
已知(1-2x)2013=a0+a1x+a2x2+a3x3+…+a2013x2013,
令x=0,可得a0=1,
令x=1,可得a0+a1+a2+a3+…+a2013=(1-2•1)2013=-1,
令x=-1,可得a0-a1+a2+a3+…-a2013=(1+2•1)2013=32013,
请仿照这种“赋值法”,求出
| a1 |
| 2 |
| a2 |
| 22 |
| a3 |
| 23 |
| a2013 |
| 22013 |
-1
-1
.函数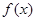 的定义域为
的定义域为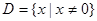 ,且满足对于任意
,且满足对于任意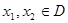 ,有
,有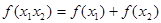 .
.
⑴求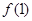 的值;
的值;
⑵判断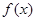 的奇偶性并证明;
的奇偶性并证明;
⑶如果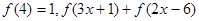 ≤
≤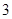 ,且
,且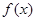 在
在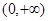 上是增函数,求
上是增函数,求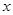 的取值范围.
的取值范围.
【解析】(Ⅰ) 通过赋值法,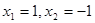 ,求出f(1)0;
,求出f(1)0;
(Ⅱ) 说明函数f(x)的奇偶性,通过令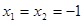 ,得
,得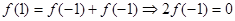 .令
.令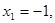
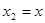 ,得
,得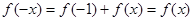 ,推出对于任意的x∈R,恒有f(-x)=f(x),f(x)为偶函数.
,推出对于任意的x∈R,恒有f(-x)=f(x),f(x)为偶函数.
(Ⅲ) 推出函数的周期,根据函数在[-2,2]的图象以及函数的周期性,即可求满足f(2x-1)≥12的实数x的集合.
查看习题详情和答案>>
观察下列问题:
已知(1-2x)2013=a0+a1x+a2x2+a3x3+…+a2013x2013,
令x=0,可得a0=1,
令x=1,可得a0+a1+a2+a3+…+a2013=(1-2•1)2013=-1,
令x=-1,可得a0-a1+a2+a3+…-a2013=(1+2•1)2013=32013,
请仿照这种“赋值法”,求出
+
+
+…+
=______.
查看习题详情和答案>>
已知(1-2x)2013=a0+a1x+a2x2+a3x3+…+a2013x2013,
令x=0,可得a0=1,
令x=1,可得a0+a1+a2+a3+…+a2013=(1-2•1)2013=-1,
令x=-1,可得a0-a1+a2+a3+…-a2013=(1+2•1)2013=32013,
请仿照这种“赋值法”,求出
| a1 |
| 2 |
| a2 |
| 22 |
| a3 |
| 23 |
| a2013 |
| 22013 |
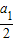
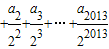 = .
= . 的展开式中,前三项系数的绝对值成等差数列
的展开式中,前三项系数的绝对值成等差数列