摘要:(3) 设实数.求函数在上的最小值
网址:http://m.1010jiajiao.com/timu_id_150277[举报]
已知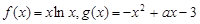
(1)求函数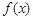 在
在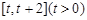 上的最小值
上的最小值
(2)对一切的 恒成立,求实数a的取值范围
恒成立,求实数a的取值范围
(3)证明对一切 ,都有
,都有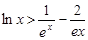 成立
成立
【解析】第一问中利用
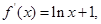 当
当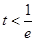 时,
时,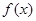 在
在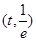 单调递减,在
单调递减,在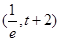 单调递增
单调递增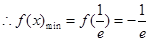 ,当
,当
 ,即
,即 时,
时,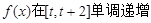 ,
,
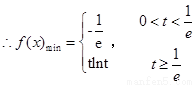
第二问中,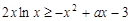 ,则
,则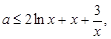 设
设 ,
,
则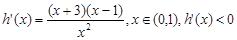 ,
, 单调递增,
单调递增, ,
, ,
, 单调递减,
单调递减,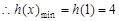 ,因为对一切
,因为对一切 ,
,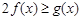 恒成立,
恒成立,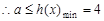
第三问中问题等价于证明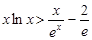 ,
, ,
,
由(1)可知 ,
, 的最小值为
的最小值为 ,当且仅当x=
,当且仅当x= 时取得
时取得
设 ,
, ,则
,则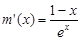 ,易得
,易得
 。当且仅当x=1时取得.从而对一切
。当且仅当x=1时取得.从而对一切 ,都有
,都有 成立
成立
解:(1)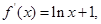 当
当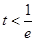 时,
时,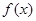 在
在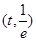 单调递减,在
单调递减,在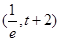 单调递增
单调递增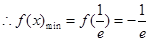 ,当
,当
 ,即
,即 时,
时,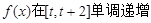 ,
,
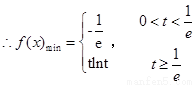 …………4分
…………4分
(2)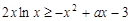 ,则
,则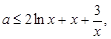 设
设 ,
,
则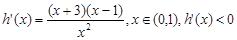 ,
, 单调递增,
单调递增, ,
, ,
, 单调递减,
单调递减,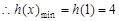 ,因为对一切
,因为对一切 ,
,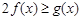 恒成立,
恒成立,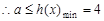 …………9分
…………9分
(3)问题等价于证明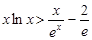 ,
, ,
,
由(1)可知 ,
, 的最小值为
的最小值为 ,当且仅当x=
,当且仅当x= 时取得
时取得
设 ,
, ,则
,则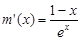 ,易得
,易得
 。当且仅当x=1时取得.从而对一切
。当且仅当x=1时取得.从而对一切 ,都有
,都有 成立
成立
查看习题详情和答案>>
函数f(x)=x3+
ax2+x+1(x∈R).
(1)若f(x)在x∈(-∞,+∞)上是增函数,求实数a的取值范围;
(2)在(1)的条件下,设g(x)=e2x-aex,x∈[0,ln2],求函数g(x)的最小值;
(3)当a=0时,曲线y=f(x)的切线的斜率的取值范围记为集合A,曲线y=f(x)上不同两点P(x1,y1),Q(x2,y2)连线的斜率的取值范围记为集合B,你认为集合A,B之间有怎样的关系,并证明你的结论.
查看习题详情和答案>>
| 1 | 2 |
(1)若f(x)在x∈(-∞,+∞)上是增函数,求实数a的取值范围;
(2)在(1)的条件下,设g(x)=e2x-aex,x∈[0,ln2],求函数g(x)的最小值;
(3)当a=0时,曲线y=f(x)的切线的斜率的取值范围记为集合A,曲线y=f(x)上不同两点P(x1,y1),Q(x2,y2)连线的斜率的取值范围记为集合B,你认为集合A,B之间有怎样的关系,并证明你的结论.