摘要:两边平方得.即.
网址:http://m.1010jiajiao.com/timu_id_147062[举报]
某工厂有旧墙一面长
14m,现准备利用这面旧墙建平面图形为矩形,面积为126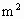 的厂房.工程条件是①建1m新墙的费用为a元;②修1m旧墙的费用为
的厂房.工程条件是①建1m新墙的费用为a元;②修1m旧墙的费用为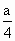 元;③拆去1m旧墙,用所得材料建1m新墙的费用为
元;③拆去1m旧墙,用所得材料建1m新墙的费用为 元.经讨论有两种方案:(1)利用旧墙的一段x m(x<14)为矩形厂房的一面边长;(2)矩形厂房的一面长x≥14,问如何利用旧墙即x为多少时建墙费用最省?(1)、(2)两种方案哪种方案最好?
查看习题详情和答案>>
元.经讨论有两种方案:(1)利用旧墙的一段x m(x<14)为矩形厂房的一面边长;(2)矩形厂房的一面长x≥14,问如何利用旧墙即x为多少时建墙费用最省?(1)、(2)两种方案哪种方案最好?
查看习题详情和答案>>
某工厂有旧墙一面长14m,现准备利用这面旧墙建平面图形为矩形,面积为126 的厂房.工程条件是①建1m新墙的费用为a元;②修1m旧墙的费用为
的厂房.工程条件是①建1m新墙的费用为a元;②修1m旧墙的费用为 元;③拆去1m旧墙,用所得材料建1m新墙的费用为
元;③拆去1m旧墙,用所得材料建1m新墙的费用为 元.经讨论有两种方案:(1)利用旧墙的一段x m(x<14)为矩形厂房的一面边长;(2)矩形厂房的一面长x≥14,问如何利用旧墙即x为多少时建墙费用最省?(1)、(2)两种方案哪种方案最好?
元.经讨论有两种方案:(1)利用旧墙的一段x m(x<14)为矩形厂房的一面边长;(2)矩形厂房的一面长x≥14,问如何利用旧墙即x为多少时建墙费用最省?(1)、(2)两种方案哪种方案最好?
课外研究题:将一块圆心角为![]() ,半径为20厘米的扇形铁片裁成一块矩形,请你设计裁法,使裁得矩形的面积最大?并说明理由.
,半径为20厘米的扇形铁片裁成一块矩形,请你设计裁法,使裁得矩形的面积最大?并说明理由.
教学建议:这是一个研究性学习内容,可让学生在课外两人一组合作完成,写成研究报告,在习题课上让学生交流研究结果,老师可适当进行点评。
参考答案:这是一个如何下料的问题,一般有如图(1)、图(2)的两种裁法:即让矩形一边在扇形的一条半径![]() 上,或让矩形一边与弦
上,或让矩形一边与弦![]() 平行。从图形的特点来看,涉及到线段的长度和角度,将这些量放置在三角形中,通过解三角形求出矩形的边长,再计算出两种方案所得矩形的最大面积,加以比较,
平行。从图形的特点来看,涉及到线段的长度和角度,将这些量放置在三角形中,通过解三角形求出矩形的边长,再计算出两种方案所得矩形的最大面积,加以比较,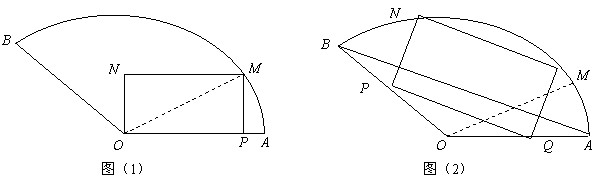 就可以得出问题的结论.
就可以得出问题的结论.
线段AB的中点O也是线段AB的重心,O具有以下性质:①O平分线段AB的长度;②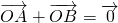 ③O是直线AB上所有点中到线段AB两个端点的距离的平方和最小的点.由此推广到三角形,设△ABC的重心为G,我们得到如下猜想:
③O是直线AB上所有点中到线段AB两个端点的距离的平方和最小的点.由此推广到三角形,设△ABC的重心为G,我们得到如下猜想:
A.G平分△ABC的面积(即△GAB、△GBC、△GAC面积相等);
B.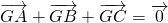
C.G是平面ABC内所有点中到△ABC三边的距离的平方和最小的点;
D.G是平面ABC内所有点中到△ABC三个顶点的距离的平方和最小的点;
你认为正确的猜想有________(填上所有你认为正确的猜想的序号).
查看习题详情和答案>>
拓展探究题
(1)已知两个圆:①x2+y2=1;②x2+(y-3)2=1,则由①式减去②式可得两圆的对称轴方程.将上述命题在曲线仍为圆的情况下加以推广,即要求得到一个更一般的命题,而已知命题应成为所推广命题的一个特例.推广的命题为
(2)平面几何中有正确命题:“正三角形内任意一点到三边的距离之和等于定值,大小为边长的
倍”,请你写出此命题在立体几何中类似的真命题:
查看习题详情和答案>>
(1)已知两个圆:①x2+y2=1;②x2+(y-3)2=1,则由①式减去②式可得两圆的对称轴方程.将上述命题在曲线仍为圆的情况下加以推广,即要求得到一个更一般的命题,而已知命题应成为所推广命题的一个特例.推广的命题为
已知两个圆:①(x-a)2+(y-b)2=r2;②(x-c)2+(y-d)2=r2,则由①式减去②式可得两圆的对称轴方程
已知两个圆:①(x-a)2+(y-b)2=r2;②(x-c)2+(y-d)2=r2,则由①式减去②式可得两圆的对称轴方程
.(2)平面几何中有正确命题:“正三角形内任意一点到三边的距离之和等于定值,大小为边长的
| ||
| 2 |
正四面体内任意一点到四个面的距离之和是一个定值,大小为棱长的
倍
| ||
| 3 |
正四面体内任意一点到四个面的距离之和是一个定值,大小为棱长的
倍
.
| ||
| 3 |