摘要： 解:(1)解:设为函数图像的一个对称点.则对于恒成立. 即对于恒成立.-----由.故函数图像的一个对称点为. --------是奇函数.不存在常数a使 x∈[-1.1] 时恒成立.依题.此时令 x∈[-1.1]∴∈［-7.1］若a=0,＝0.不合题,若a>0, 此时为单调增函数.＝-a.若存在a合题.则-a1,与a>0矛盾.若a<0, 此时为单调减函数. ＝a若存在a合题.则a1.与a<0矛盾.综上可知.符合条件的a不存在. ----------------10分(3)函数的图像关于直线对称的充要条件是--------------------------①时..其图像关于轴上任意一点成中心对称,关于平行于轴的任意一条直线成轴对称图形,②时..其图像关于轴对称图形,③时..其图像关于原点中心对称,④时.的图像不可能是轴对称图形.设为函数图像的一个对称点.则对于恒成立. 即对于恒成立.由.故函数图像的一个对称点为. ------
网址：http://m.1010jiajiao.com/timu_id_128649[举报]
设函数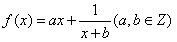
，曲线y=f（x）在点（2，f（2））处的切线方程为y=3，
（Ⅰ）求f（x）的解析式；
（Ⅱ）证明：函数y=f（x）的图像是一个中心对称图形，并求其对称中心；
（Ⅲ）证明：曲线y=f（x）上任一点的切线与直线x=1和直线y=x所围三角形的面积为定值，并求出此定值。
查看习题详情和答案>>
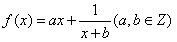，曲线y=f（x）在点（2，f（2））处的切线方程为y=3，（Ⅰ）求f（x）的解析式；
（Ⅱ）证明：函数y=f（x）的图像是一个中心对称图形，并求其对称中心；
（Ⅲ）证明：曲线y=f（x）上任一点的切线与直线x=1和直线y=x所围三角形的面积为定值，并求出此定值。
设函数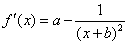
，曲线
在点
处的切线方程为
，曲线在点处的切线方程为
。（1）求
的解析式；（2）证明：曲线
的图像是一个中心对称图形，并求其对称中心；（3）证明：曲线
上任一点处的切线与直线
和直线
所围三角形的面积为定值，并求出此定值。
设函数
，曲线y＝f(x)在点(2，f(2))处的切线方程为y＝3．
(Ⅰ)求y＝f(x)的解析式：
(Ⅱ)证明：函数y＝f(x)的图像是一个中心对称图形，并求其对称中心；
(Ⅲ)证明：曲线y＝f(x)上任一点的切线与直线x＝1和直线y＝x所围三角形的面积为定值，并求出此定值．
(a，b∈Z)，曲线y＝f(x)在点(0，f(2))处的切线方程为y＝3．
，如果存在实数
使得
，那么称
为
的生成函数．
；
；
，生成函数
在
上有解，求实数
的取值范围；
，取
，生成函数
．若对于任意正实数
且
．试问是否存在最大的常数
，使
恒成立？如果存在，求出这个