网址:http://m.1010jiajiao.com/timu_id_117155[举报]
说明
1. 本解答列出试题的一种或几种解法,如果考生的解法与所列解法不同,可参照解答中评分标准的精神进行评分.
2. 评阅试卷,应坚持每题评阅到底,不要因为考生的解答中出现错误而中断对该题的评阅. 当考生的解答在某一步出现错误,影响了后继部分,但该步以后的解答未改变这一题的内容和难度时,可视影响程度决定后面部分的给分,这时原则上不应超过后面部分应给分数之半,如果有较严重的概念性错误,就不给分.
3. 第17题至第21题中右端所注分数,表示考生正确做到这一步应得的该题累加分数.
4. 给分或扣分均以1分为单位.
答案及评分标准
1.试题2009.04.15.files/image162.gif) ;
2.
;
2.试题2009.04.15.files/image164.gif) ; 3.
; 3.试题2009.04.15.files/image166.gif) ;
4.
;
4.试题2009.04.15.files/image168.gif) ; 5.(理)
; 5.(理)试题2009.04.15.files/image170.gif) 元;(文)0.7;
元;(文)0.7;
6.(理)试题2009.04.15.files/image172.gif) ; (文)200赫兹; 7.(理)5; (文)p=4.
; (文)200赫兹; 7.(理)5; (文)p=4.
8.(理)试题2009.04.15.files/image174.gif) ; (文)
; (文)试题2009.04.15.files/image176.gif)
9.试题2009.04.15.files/image178.gif) ; 10.(理)
; 10.(理)试题2009.04.15.files/image180.gif) ; (文)方程为
; (文)方程为试题2009.04.15.files/image182.gif) .
.
11.(理)试题2009.04.15.files/image184.gif) ; (文)
; (文)试题2009.04.15.files/image186.gif) ; 12.12.
; 12.12.
13――16:A; C ; C; 理B文A
17.设熊猫居室的总面积为试题2009.04.15.files/image154.gif) 平方米,由题意得:
平方米,由题意得:试题2009.04.15.files/image189.gif) .… 6分
.… 6分
解法1:试题2009.04.15.files/image191.gif) ,因为
,因为试题2009.04.15.files/image193.gif) ,而当
,而当试题2009.04.15.files/image195.gif) 时,
时,试题2009.04.15.files/image154.gif) 取得最大值75. 10分
取得最大值75. 10分
所以当熊猫居室的宽为
解法2:试题2009.04.15.files/image198.gif) =75,当且仅当
=75,当且仅当试题2009.04.15.files/image200.gif) ,即
,即试题2009.04.15.files/image195.gif) 时,
时,试题2009.04.15.files/image154.gif) 取得最大值75.
…… 10分
取得最大值75.
…… 10分
所以当熊猫居室的宽为
18.理:如图,建立空间直角坐标系,可得有关点的坐标为试题2009.04.15.files/image202.gif) 、
、试题2009.04.15.files/image204.gif) 、
、试题2009.04.15.files/image206.gif) 、
、试题2009.04.15.files/image208.gif) 、
、试题2009.04.15.files/image210.gif) 、
、试题2009.04.15.files/image212.gif) .
……2分
.
……2分
设平面试题2009.04.15.files/image214.gif) 的法向量为
的法向量为试题2009.04.15.files/image216.gif) ,则
,则试题2009.04.15.files/image218.gif) ,
,试题2009.04.15.files/image220.gif) .
.
因为试题2009.04.15.files/image222.gif) ,
,试题2009.04.15.files/image224.gif) ,
……3分
,
……3分
试题2009.04.15.files/image226.gif) ,
,试题2009.04.15.files/image228.gif) ,
,
所以试题2009.04.15.files/image230.gif) 解得
解得试题2009.04.15.files/image232.gif) ,取
,取试题2009.04.15.files/image234.gif) ,得平面
,得平面试题2009.04.15.files/image214.gif) 一个法向量
一个法向量试题2009.04.15.files/image236.gif) ,且
,且试题2009.04.15.files/image238.gif) .
……5分
.
……5分
(1)在平面试题2009.04.15.files/image214.gif) 取一点
取一点试题2009.04.15.files/image145.gif) ,可得
,可得试题2009.04.15.files/image240.gif) ,于是顶点
,于是顶点试题2009.04.15.files/image242.gif) 到平面
到平面试题2009.04.15.files/image214.gif) 的距离
的距离试题2009.04.15.files/image244.gif) ,所以顶点
,所以顶点试题2009.04.15.files/image242.gif) 到平面
到平面试题2009.04.15.files/image214.gif) 的距离为
的距离为试题2009.04.15.files/image246.gif) ,
……8分
,
……8分
(2)因为平面试题2009.04.15.files/image248.gif) 的一个法向量为
的一个法向量为试题2009.04.15.files/image250.gif) ,设
,设试题2009.04.15.files/image252.gif) 与
与试题2009.04.15.files/image254.gif) 的夹角为a,则
的夹角为a,则
试题2009.04.15.files/image256.gif) ,
……12分
,
……12分
结合图形可判断得二面角试题2009.04.15.files/image258.gif) 是一个锐角,它的大小为
是一个锐角,它的大小为试题2009.04.15.files/image260.gif) .……14分
.……14分
试题2009.04.15.files/image265.gif)
试题2009.04.15.files/image266.gif)
文:(1)圆锥底面积为试题2009.04.15.files/image268.gif) cm2,
……1分
cm2,
……1分
设圆锥高为试题2009.04.15.files/image270.gif) cm,由体积
cm,由体积试题2009.04.15.files/image272.gif) ,
……5分
,
……5分
由试题2009.04.15.files/image274.gif) cm3得
cm3得试题2009.04.15.files/image276.gif) cm;
……8分
cm;
……8分
(2)母线长试题2009.04.15.files/image278.gif) cm,
……9分
cm,
……9分
设底面周长为试题2009.04.15.files/image280.gif) ,则该圆锥的侧面积=
,则该圆锥的侧面积=试题2009.04.15.files/image282.gif) ,
……12分
,
……12分
所以该圆锥的侧面积=试题2009.04.15.files/image284.gif) cm2.
……14分
cm2.
……14分
19.(理)(1)试题2009.04.15.files/image286.gif) ;
……3分
;
……3分
(2)当试题2009.04.15.files/image288.gif) 时,(
时,(试题2009.04.15.files/image290.gif) )
)
试题2009.04.15.files/image292.gif) ,
……6分
,
……6分
所以,试题2009.04.15.files/image294.gif) (
(试题2009.04.15.files/image114.gif) ).
……8分
).
……8分
(3)与(2)同理可求得:试题2009.04.15.files/image297.gif) ,
……10分
,
……10分
设试题2009.04.15.files/image299.gif) =
=试题2009.04.15.files/image301.gif) ,
,
则试题2009.04.15.files/image303.gif) ,(用等比数列前n项和公式的推导方法)
,(用等比数列前n项和公式的推导方法)试题2009.04.15.files/image305.gif) ,相减得
,相减得
试题2009.04.15.files/image307.gif) ,所以
,所以
试题2009.04.15.files/image309.gif) .
……14分
.
……14分
(文)(1)设数列前试题2009.04.15.files/image118.gif) 项和为
项和为试题2009.04.15.files/image311.gif) ,则
,则试题2009.04.15.files/image313.gif) . ……3分
. ……3分
(2)公比试题2009.04.15.files/image315.gif) ,所以由无穷等比数列各项的和公式得:
,所以由无穷等比数列各项的和公式得:
数列试题2009.04.15.files/image108.gif) 各项的和为
各项的和为试题2009.04.15.files/image318.gif) =1.
……7分
=1.
……7分
(3)设数列试题2009.04.15.files/image122.gif) 的前
的前试题2009.04.15.files/image118.gif) 项和为
项和为试题2009.04.15.files/image301.gif) ,当
,当试题2009.04.15.files/image118.gif) 为奇数时,
为奇数时,试题2009.04.15.files/image321.gif) =
=
试题2009.04.15.files/image323.gif) ;
……11分
;
……11分
当试题2009.04.15.files/image118.gif) 为偶数时,
为偶数时,试题2009.04.15.files/image325.gif) =
=试题2009.04.15.files/image327.gif) . ……14分
. ……14分
即试题2009.04.15.files/image329.gif) .
……15分
.
……15分
20.(1)试题2009.04.15.files/image135.gif) 即
即试题2009.04.15.files/image331.gif) ,又
,又试题2009.04.15.files/image333.gif) ,2分
,2分
所以试题2009.04.15.files/image335.gif) ,从而
,从而试题2009.04.15.files/image127.gif) 的取值范围是
的取值范围是试题2009.04.15.files/image337.gif) .
……5分
.
……5分
(2)试题2009.04.15.files/image339.gif) ,令
,令试题2009.04.15.files/image341.gif) ,则
,则试题2009.04.15.files/image343.gif) ,因为
,因为试题2009.04.15.files/image137.gif) ,所以
,所以试题2009.04.15.files/image346.gif) ,当且仅当
,当且仅当试题2009.04.15.files/image348.gif) 时,等号成立,8分
时,等号成立,8分
由试题2009.04.15.files/image350.gif) 解得
解得试题2009.04.15.files/image352.gif) ,所以当
,所以当试题2009.04.15.files/image354.gif) 时,函数
时,函数试题2009.04.15.files/image139.gif) 的最小值是
的最小值是试题2009.04.15.files/image356.gif) ; ……11分
; ……11分
下面求当试题2009.04.15.files/image358.gif) 时,函数
时,函数试题2009.04.15.files/image139.gif) 的最小值.
的最小值.
当试题2009.04.15.files/image358.gif) 时,
时,试题2009.04.15.files/image360.gif) ,函数
,函数试题2009.04.15.files/image362.gif) 在
在试题2009.04.15.files/image364.gif) 上为减函数.所以函数
上为减函数.所以函数试题2009.04.15.files/image139.gif) 的最小值为
的最小值为试题2009.04.15.files/image366.gif) .
.
[当试题2009.04.15.files/image358.gif) 时,函数
时,函数试题2009.04.15.files/image362.gif) 在
在试题2009.04.15.files/image364.gif) 上为减函数的证明:任取
上为减函数的证明:任取试题2009.04.15.files/image369.gif) ,
,试题2009.04.15.files/image371.gif) ,因为
,因为试题2009.04.15.files/image373.gif) ,
,试题2009.04.15.files/image375.gif) ,所以
,所以试题2009.04.15.files/image377.gif) ,
,试题2009.04.15.files/image379.gif) ,由单调性的定义函数
,由单调性的定义函数试题2009.04.15.files/image362.gif) 在
在试题2009.04.15.files/image364.gif) 上为减函数.]
上为减函数.]
于是,当试题2009.04.15.files/image354.gif) 时,函数
时,函数试题2009.04.15.files/image139.gif) 的最小值是
的最小值是试题2009.04.15.files/image356.gif) ;当
;当试题2009.04.15.files/image358.gif) 时,函数
时,函数试题2009.04.15.files/image139.gif) 的最小值
的最小值试题2009.04.15.files/image382.gif) .
……15分
.
……15分
21.(1)由试题2009.04.15.files/image384.gif) 解得
解得试题2009.04.15.files/image386.gif) ;由
;由试题2009.04.15.files/image388.gif) 解得
解得试题2009.04.15.files/image390.gif) .
.
由点斜式写出两条直线试题2009.04.15.files/image152.gif) 的方程,
的方程,试题2009.04.15.files/image392.gif) ,
,
所以直线AB的斜率为试题2009.04.15.files/image394.gif) . ……4分
. ……4分
(2)推广的评分要求分三层
一层:点P到一般或斜率到一般,或抛物线到一般(3分,问题1分、解答2分)
例:1.已知试题2009.04.15.files/image141.gif) 是抛物线
是抛物线试题2009.04.15.files/image143.gif) 上的相异两点.设过点
上的相异两点.设过点试题2009.04.15.files/image145.gif) 且斜率为-1的直线
且斜率为-1的直线试题2009.04.15.files/image396.gif) ,与过点
,与过点试题2009.04.15.files/image074.gif) 且斜率为1的直线
且斜率为1的直线试题2009.04.15.files/image398.gif) 相交于抛物线
相交于抛物线试题2009.04.15.files/image143.gif) 上的一定点P
上的一定点P试题2009.04.15.files/image400.gif) ,求直线AB的斜率;
,求直线AB的斜率;
2.已知试题2009.04.15.files/image141.gif) 是抛物线
是抛物线试题2009.04.15.files/image143.gif) 上的相异两点.设过点
上的相异两点.设过点试题2009.04.15.files/image145.gif) 且斜率为-k 1的直线
且斜率为-k 1的直线试题2009.04.15.files/image396.gif) ,与过点
,与过点试题2009.04.15.files/image074.gif) 且斜率为k的直线
且斜率为k的直线试题2009.04.15.files/image398.gif) 相交于抛物线
相交于抛物线试题2009.04.15.files/image143.gif) 上的一点P(4,4),求直线AB的斜率;
上的一点P(4,4),求直线AB的斜率;
3.已知试题2009.04.15.files/image141.gif) 是抛物线
是抛物线试题2009.04.15.files/image402.gif) 上的相异两点.设过点
上的相异两点.设过点试题2009.04.15.files/image145.gif) 且斜率为-1的直线
且斜率为-1的直线试题2009.04.15.files/image396.gif) ,与过点
,与过点试题2009.04.15.files/image074.gif) 且斜率为1的直线
且斜率为1的直线试题2009.04.15.files/image398.gif) 相交于抛物线
相交于抛物线试题2009.04.15.files/image402.gif) 上的一定点P
上的一定点P试题2009.04.15.files/image405.gif) ,求直线AB的斜率; AB的斜率的值.
,求直线AB的斜率; AB的斜率的值.
二层:两个一般或推广到其它曲线(4分,问题与解答各占2分)
例:4.已知点R是抛物线试题2009.04.15.files/image143.gif) 上的定点.过点P作斜率分别为
上的定点.过点P作斜率分别为试题2009.04.15.files/image408.gif) 、
、试题2009.04.15.files/image410.gif) 的两条直线
的两条直线试题2009.04.15.files/image152.gif) ,分别交抛物线于A、B两点,试计算直线AB的斜率.
,分别交抛物线于A、B两点,试计算直线AB的斜率.
三层:满分(对抛物线,椭圆,双曲线或对所有圆锥曲线成立的想法.)(7分,问题3分、解答4分)
例如:5.已知抛物线试题2009.04.15.files/image412.gif) 上有一定点P,过点P作斜率分别为
上有一定点P,过点P作斜率分别为试题2009.04.15.files/image408.gif) 、
、试题2009.04.15.files/image410.gif) 的两条直线
的两条直线试题2009.04.15.files/image152.gif) ,分别交抛物线于A、B两点,试计算直线AB的斜率.
,分别交抛物线于A、B两点,试计算直线AB的斜率.
过点P(试题2009.04.15.files/image414.gif) ),斜率互为相反数的直线可设为
),斜率互为相反数的直线可设为试题2009.04.15.files/image416.gif) ,
,试题2009.04.15.files/image416.gif) ,其中
,其中试题2009.04.15.files/image419.gif) 。
。
由试题2009.04.15.files/image421.gif) 得
得试题2009.04.15.files/image423.gif) ,所以
,所以
试题2009.04.15.files/image425.gif)
同理,把上式中试题2009.04.15.files/image408.gif) 换成
换成试题2009.04.15.files/image410.gif) 得
得试题2009.04.15.files/image428.gif) ,所以
,所以
当P为原点时直线AB的斜率不存在,当P不为原点时直线AB的斜率为试题2009.04.15.files/image430.gif) 。
。
(3)(理)点试题2009.04.15.files/image156.gif) ,设
,设试题2009.04.15.files/image433.gif) ,则
,则试题2009.04.15.files/image435.gif) .
.
设线段试题2009.04.15.files/image437.gif) 的中点是
的中点是试题2009.04.15.files/image439.gif) ,斜率为
,斜率为试题2009.04.15.files/image408.gif) ,则
,则试题2009.04.15.files/image441.gif) =
=试题2009.04.15.files/image443.gif) .12分
.12分
所以线段试题2009.04.15.files/image437.gif) 的垂直平分线
的垂直平分线试题2009.04.15.files/image445.gif) 的方程为
的方程为试题2009.04.15.files/image447.gif) ,
,
又点试题2009.04.15.files/image449.gif) 在直线
在直线试题2009.04.15.files/image445.gif) 上,所以
上,所以试题2009.04.15.files/image451.gif) ,而
,而试题2009.04.15.files/image453.gif) ,于是
,于是试题2009.04.15.files/image455.gif) .
……13分
.
……13分
(斜率试题2009.04.15.files/image457.gif)
试题2009.04.15.files/image459.gif) ,则
,则试题2009.04.15.files/image461.gif) --------------------------------13分)
--------------------------------13分)
线段试题2009.04.15.files/image437.gif) 所在直线的方程为
所在直线的方程为试题2009.04.15.files/image463.gif) ,
……14分
,
……14分
代入试题2009.04.15.files/image143.gif) ,整理得
,整理得试题2009.04.15.files/image466.gif) ……15分
……15分
试题2009.04.15.files/image468.gif) ,
,试题2009.04.15.files/image470.gif) 。设
。设试题2009.04.15.files/image437.gif) 线段长为
线段长为试题2009.04.15.files/image445.gif) ,则
,则
试题2009.04.15.files/image472.gif) =
=
试题2009.04.15.files/image474.gif) ……16分
……16分
因为试题2009.04.15.files/image476.gif) ,所以
,所以试题2009.04.15.files/image478.gif) ……18分
……18分
即:试题2009.04.15.files/image480.gif) .(
.(试题2009.04.15.files/image482.gif) )
)
(文)设试题2009.04.15.files/image433.gif) ,则
,则
(本大题满分18分)本大题共有3个小题,第1小题满分4分,第2小题满6分,第3小题满8分.
已知集合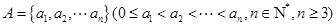 具有性质
具有性质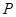 :对任意
:对任意 ,
,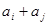 与
与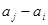 至少一个属于
至少一个属于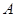 .
.
(1)分别判断集合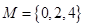 与
与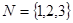 是否具有性质
是否具有性质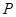 ,并说明理由;
,并说明理由;
(2)①求证: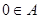 ;
;
②求证: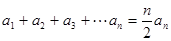 ;
;
(3)研究当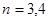 和
和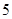 时,集合
时,集合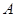 中的数列
中的数列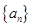 是否一定成等差数列.
是否一定成等差数列.
查看习题详情和答案>>
(本题共3小题,满分18分。第1小题满分4分,第2小题满分7分,第3小题7分)
对定义在 上,并且同时满足以下两个条件的函数
上,并且同时满足以下两个条件的函数 称为
称为 函数.
函数.
① 对任意的 ,总有
,总有 ;
;
② 当 时,总有
时,总有 成立.
成立.
已知函数 与
与 是定义在
是定义在 上的函数.
上的函数.
(1)试问函数 是否为
是否为 函数?并说明理由;
函数?并说明理由;
(2)若函数 是
是 函数,求实数
函数,求实数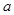 的值;
的值;
(3)在(2)的条件下,是否存在实数 ,使方程
,使方程 恰有两解?若存在,求出实数
恰有两解?若存在,求出实数 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看习题详情和答案>>
对定义在
 上,并且同时满足以下两个条件的函数
上,并且同时满足以下两个条件的函数 称为
称为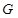 函数.
函数.① 对任意的
 ,总有
,总有 ;
;② 当
 时,总有
时,总有 成立.
成立.已知函数
 与
与 是定义在
是定义在 上的函数.
上的函数.(1)试问函数
 是否为
是否为 函数?并说明理由;
函数?并说明理由;(2)若函数
 是
是 函数,求实数
函数,求实数 的值;
的值;(3)在(2)的条件下,是否存在实数
 ,使方程
,使方程 恰有两解?若存在,求出实数
恰有两解?若存在,求出实数 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.试题2009.04.15.fi </div>
<div id=)