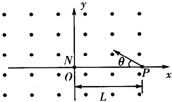如图所示，在xOy 坐标系内有垂直纸面向外的范围足够大的匀强磁场，磁感应强度的大小为B．在t=0 时刻有两个粒子N、P分别从坐标原点O及坐标（ L，0）点开始运动．N粒子带正电，电量为q，质量为m，速度大小为v_n、方向为在xOy 平面内的所有可能的方向；P粒子不带电，其速度大小为v_P．方向为在xOy 平面内且与x 轴的负方向的夹角为q．两粒子所受的重力不计．
（1）对于Vn有一临界值v，当v_n＜v 时，两个粒子不可能相遇，求临界值可的大小；
（2）若两个粒子相遇的位置在y轴上，且已知q=30°，L=

3

m，m=6.4×10^-27kg，q=3.2×10^-19 C，v_n=1.15π?10⁷m/s，v_P=3?10⁶ m/s．求v_n的方向与y 轴正方向的夹角β

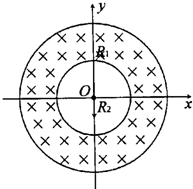如图所示，在直角坐标系xOy决定的平面内，有两个同心圆，外侧圆半径为R₁，内侧圆半径为R₂，圆心为O．两圆之间的圆环内有磁感应强度为B的匀强磁场，磁场方向垂直于纸面指向纸内．在圆心O处有一质子源，沿y轴负方向发射质子流，质子流中质子的速度范围为0～v．结果有的质子从内侧圆离开磁场，有的质子从外侧圆离开磁场．已知质子带电量为e，质量为m，不考虑质子通过磁场后再进入磁场的情况．
（1）求所有质子通过的内侧圆的孤长；
（2）质子在磁场中运动的最长时间．

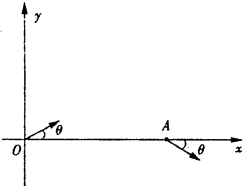如图所示，在xOy平面内，一质量为m，电荷量为q的带电粒子（重力不计）以速度v₀从坐标原点O沿与+x方向成θ角射人第一象限区，并从x轴上A的点离开第一象限区．
（1）若在xOy平面存在一点电荷形成的电场，带电粒子q在电场力作用下沿圆弧匀速率从O点运动到A点，已知OA间的距离为a，θ=30°，求O点电场强度E的大小．
（2）若只存在一范围足够大的垂直于xOy平面的匀强磁场区，已知磁场的磁感应强度为B，求带电粒子飞离y轴的最远距离．
（3）若只在第一象限内存在垂直于xOy平面的圆形匀强磁场区，已知OA间的距离仍为a，且θ=45°，求磁场的磁感应强度的最小值B₀．

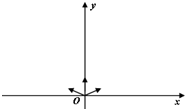如图所示，在x轴上方平面内存在方向垂直纸面向外的匀强磁场，磁感应强度大小为B．坐标原点O处有一离子源，可以在平行于纸面内向x轴上方（包括x轴）沿各个方向发射速率在0到υ_m之间、质量为m、电量为q的负离子．不计离子的重力和离子之间的相互作用力，试分析：
（1）若在t=0时刻发射的各种速率的离子仅沿+x方向，写出经过t=

πn

2qB

时这些离子所在位置的坐标y与x的关系式和范围．
（2）若在x轴的上方距离x轴d=

8mmv

5qB

处放一足够长的屏，屏与x轴平行，离子以最大速度υ_m向x轴上方各个方向发射，求这些离子打在屏上的范围．
（3）若从t=0时刻开始向x轴上方各个方向发射各种速率的离子，求从t=0到t=

πn

2qB

时间内所有离子可能到达过的位置所组成区域的最大面积．

如图所示，在0≤x≤a，0≤y≤2a范围内有垂直于xy平面向内的匀强磁场，在a＜x≤2a，0≤y≤2a范围内有垂直于xy平面向外的匀强磁场，磁场的磁感应强度大小均为B．坐标原点O处有一个粒子源，在某时刻发射大量质量为m、电荷量为q的带正电粒子，它们的速度大小相同，速度方向均在xy平面内，与y轴正方向夹角分布在0-90°范围内，已知从（0，2a）处射出的带电粒子在磁场中运动的时间恰好为粒子在磁场中做圆周运动周期的四分之一．不计粒子重力及粒子之间相互作用，求：
（1）粒子进入磁场中的速度大小？
（2）沿x轴正方向入射的粒子和最后离开磁场的粒子在磁场中运动的时间之差为多少？