摘要：即有最大值为32.
网址：http://m.1010jiajiao.com/timu_id_107919[举报]
一段长为32米的篱笆围成一个一边靠墙的矩形菜园，墙长18米，问这个矩形的长、宽各为多少时，菜园的面积最大，最大面积是多少？
【解析】解：令矩形与墙垂直的两边为宽并设矩形宽为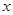
，则长为
所以矩形的面积
（
） （4分
=128 （8分）
当且仅当
时，即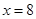
时等号成立，此时
有最大值128
所以当矩形的长为=16，宽为8时，
菜园面积最大，最大面积为128 （13分）答：当矩形的长为16米，宽为8米时。菜园面积最大，最大面积为128平方米（注：也可用二次函数模型解答）
查看习题详情和答案>>
某同学探究函数f(x)=x+
（x＞0）的最小值，并确定相应的x的值．先列表如下：
请观察表中y值随x值变化的特点，完成下列问题：（（1）（2）问的填空只要写出结果即可）
（1）若x1x2=4，则 f（x1）______f（x2）．（请填写“＞，=，＜”号）；若函数f(x)=x+
（x＞0）在区间 （0，2）上递减，则f（x）在区间______ 上递增；
（2）当x=______时，f(x)=x+
（x＞0）的最小值为______；
（3）根据函数f（x）的有关性质，你能得到函数f(x)=x+
（x＜0）的最大值吗？为什么？
查看习题详情和答案>>
| 4 |
| x |
| x | … |
|
|
1 |
|
2 |
|
4 | 8 | 16 | … | ||||||||
| y | … | 16.25 | 8.5 | 5 |
|
4 |
|
5 | 8.5 | 16.25 | … |
（1）若x1x2=4，则 f（x1）______f（x2）．（请填写“＞，=，＜”号）；若函数f(x)=x+
| 4 |
| x |
（2）当x=______时，f(x)=x+
| 4 |
| x |
（3）根据函数f（x）的有关性质，你能得到函数f(x)=x+
| 4 |
| x |
某同学探究函数f(x)=x+
（x＞0）的最小值，并确定相应的x的值．先列表如下：
请观察表中y值随x值变化的特点，完成下列问题：（（1）（2）问的填空只要写出结果即可）
（1）若x1x2=4，则 f（x1）
（x＞0）在区间 （0，2）上递减，则f（x）在区间
（2）当x=
（x＞0）的最小值为
（3）根据函数f（x）的有关性质，你能得到函数f(x)=x+
（x＜0）的最大值吗？为什么？
查看习题详情和答案>>
| 4 |
| x |
| x | … |
|
|
1 |
|
2 |
|
4 | 8 | 16 | … | ||||||||
| y | … | 16.25 | 8.5 | 5 |
|
4 |
|
5 | 8.5 | 16.25 | … |
（1）若x1x2=4，则 f（x1）
=
=
f（x2）．（请填写“＞，=，＜”号）；若函数f(x)=x+| 4 |
| x |
（2，+∞）
（2，+∞）
上递增；（2）当x=
2
2
时，f(x)=x+| 4 |
| x |
4
4
；（3）根据函数f（x）的有关性质，你能得到函数f(x)=x+
| 4 |
| x |