摘要:例12 直线的方程为.其中,椭圆的中心为.焦点在轴上.长半轴为2.短半轴为1.它的一个顶点为.问在什么范围内取值时.椭圆上有四个不同的点.它们中的每一点到点的距离等于该点到直线的距离.思路分析 从题目的要求及解析几何的知识可知.四个不同的点应在抛物线
网址:http://m.1010jiajiao.com/timu_id_105387[举报]
直线![]() 的方程为
的方程为![]() ,其中
,其中![]() ;椭圆
;椭圆![]() 的中心为
的中心为![]() ,焦点在
,焦点在![]() 轴上,长半轴为2,短半轴为1,它的一个顶点为
轴上,长半轴为2,短半轴为1,它的一个顶点为![]() ,问
,问![]() 在什么范围内取值时,椭圆上有四个不同的点,它们中的每一点到点
在什么范围内取值时,椭圆上有四个不同的点,它们中的每一点到点![]() 的距离等于该点到直线
的距离等于该点到直线![]() 的距离。
的距离。
椭圆的中心在原点,其左焦点为F(-
,0),左准线l的方程为x=-
.PQ是过点F且与x轴不垂直的弦,PQ的中点M到左准线l的距离为d.
(1)求此椭圆的方程;
(2)求证:
为定值;
(3)在l上是否存在点R,使△PQR为正三角形?若存在,求出点R的坐标;若不存在,请说明理由.
查看习题详情和答案>>
| 2 |
3
| ||
| 2 |
(1)求此椭圆的方程;
(2)求证:
| PQ |
| d |
(3)在l上是否存在点R,使△PQR为正三角形?若存在,求出点R的坐标;若不存在,请说明理由.
椭圆的中心在原点,焦点在x轴上,离心率为![]() ,△ABM的三个顶点都在椭圆上,其中点M坐标为(1,1),且直线MA、MB的斜率之和为0.
,△ABM的三个顶点都在椭圆上,其中点M坐标为(1,1),且直线MA、MB的斜率之和为0.
(Ⅰ)求椭圆的方程;
(Ⅱ)求证:直线AB的斜率是定值.
 的中心和抛物线
的中心和抛物线 的顶点均为原点
的顶点均为原点 ,
, 轴上,过
轴上,过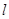 ,与
,与

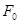 为
为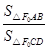 的最小值;
的最小值;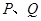 是
是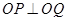 ,求证:
,求证: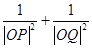 为定值;反之,当
为定值;反之,当