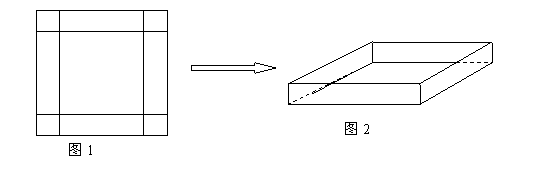
摘要：思路分析 要求的最大值.由已知条件很快将变为一元二次函数然后求极值点的值.联系到.这一条件.既快又准地求出最大值.上述解法观察到了隐蔽条件.体现了思维的变通性.思维障碍 大部分学生的作法如下:
网址：http://m.1010jiajiao.com/timu_id_105349[举报]
在一次数学实践活动课上，老师给一个活动小组安排了这样的一个任务：设计一个方案，将一块边长为4米的正方形铁片，通过裁剪、拼接的方式，将它焊接成容积至少有5立方米的长方体无盖容器（只有一个下底面和侧面的长方体）．该活动小组接到任务后，立刻设计了一个方案，如下图所示，按图1在正方形铁片的四角裁去四个相同的小正方形后，将剩下的部分焊接成长方体（如图2）．请你分析一下他们的设计方案切去边长为多大的小正方形后能得到的最大容积，最大容积是多少？是否符合要求？若不符合，请你帮他们再设计一个能符合要求的方案，简单说明操作过程和理由．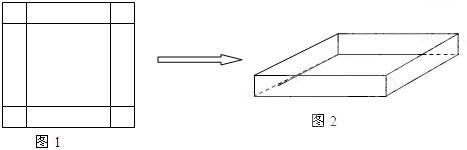
查看习题详情和答案>>
查看习题详情和答案>>
若a＞b＞c，则
+
≥
证明：因为（a-c）(
+
)=（a-b+b-c）(
+
)=2+
+
∵a＞b＞c∴a-b＞0，b-c＞0；
∴
+
≥2
=2
∴2+
+
≥4∴（a-c）(
+
)≥4
因为a＞c所以a-c＞0
所以
+
≥
类比上述命题及证明思路，回答以下问题：
①若a＞b＞c＞d，比较
+
+
与
的大小，并证明你的猜想；
②若a＞b＞c＞d＞e，且
+
+
+
≥
恒成立，试猜想m的最大值，并写出猜想过程，不要求证明．
查看习题详情和答案>>
| 1 |
| a-b |
| 1 |
| b-c |
| 4 |
| a-c |
证明：因为（a-c）(
| 1 |
| a-b |
| 1 |
| b-c |
| 1 |
| a-b |
| 1 |
| b-c |
| b-c |
| a-b |
| a-b |
| b-c |
∵a＞b＞c∴a-b＞0，b-c＞0；
∴
| b-c |
| a-b |
| a-b |
| b-c |
|
∴2+
| b-c |
| a-b |
| a-b |
| b-c |
| 1 |
| a-b |
| 1 |
| b-c |
因为a＞c所以a-c＞0
所以
| 1 |
| a-b |
| 1 |
| b-c |
| 4 |
| a-c |
类比上述命题及证明思路，回答以下问题：
①若a＞b＞c＞d，比较
| 1 |
| a-b |
| 1 |
| b-c |
| 1 |
| c-d |
| 9 |
| a-d |
②若a＞b＞c＞d＞e，且
| 1 |
| a-b |
| 1 |
| b-c |
| 1 |
| c-d |
| 1 |
| d-e |
| m |
| a-e |
（本小题满分15分）在一次数学实践活动课上，老师给一个活动小组安排了这样的一个任务：设计一个方案，将一块边长为4米的正方形铁片，通过裁剪、拼接的方式，将它焊接成容积至少有5立方米的长方体无盖容器（只有一个下底面和侧面的长方体）.该活动小组接到任务后，立刻设计了一个方案，如下图所示，按图1在正方形铁片的四角裁去四个相同的小正方形后，将剩下的部分焊接成长方体(如图2).请你分析一下他们的设计方案切去边长为多大的小正方形后能得到的最大容积，最大容积是多少？是否符合要求？若不符合，请你帮他们再设计一个能符合要求的方案，简单说明操作过程和理由. W ww.k s 5u.c om
