摘要：(Ⅲ) 试问,ㄓ能否是等腰三角形?若能,求ㄓ面积的最大值;若不能,请说明理由． 2008届高三调研考试数学试题答案及评分标准题号9101112131415答案
网址：http://m.1010jiajiao.com/timu_id_101456[举报]
某鱼塘2009年初有鱼10（万条），每年年终将捕捞当年鱼总量的50%，在第二年年初又将有一部分新鱼放入鱼塘．根据养鱼的科学技术知识，该鱼塘中鱼的总量不能超过19.5（万条）（不考虑鱼的自然繁殖和死亡等因素对鱼总量的影响），所以该鱼塘采取对放入鱼塘的新鱼数进行控制，该鱼塘每年只放入新鱼b（万条）．
（I）设第n年年初该鱼塘的鱼总量为an（年初已放入新鱼b（万条），2010年为第一年），求a1及an+1与an间的关系；
（Ⅱ）当b=10时，试问能否有效控制鱼塘总量不超过19.5（万条）？若有效，说明理由；若无效，请指出哪一年初开始鱼塘中鱼的总量超过19.5（万条）． 查看习题详情和答案>>
（I）设第n年年初该鱼塘的鱼总量为an（年初已放入新鱼b（万条），2010年为第一年），求a1及an+1与an间的关系；
（Ⅱ）当b=10时，试问能否有效控制鱼塘总量不超过19.5（万条）？若有效，说明理由；若无效，请指出哪一年初开始鱼塘中鱼的总量超过19.5（万条）． 查看习题详情和答案>>
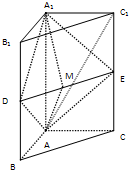如图，在直三棱柱ABC-A1B1C1中，AB⊥AC，AB=AC=1，AA1=2，D、E分别是BB1、CC1的中点，M是DE的中点．（1）求证：平面ADE⊥平面AMA1；
（2）试问能否在线段AC1上找一点N，使得直线MN与平面ADA1平行？请说明理由；
（3）求三棱锥A1-ADE的体积．
试问能否找到一条斜率为k（k≠0）的直线l与椭圆
+y2=1交于两个不同点M，N，且使M，N，且使M，N到点A（0，1）的距离相等，若存在，试求出k的取值范围；若不存在，请说明理由．
查看习题详情和答案>>
| x2 | 3 |
按照某学者的理论，假设一个人生产某产品单件成本为a元，如果他卖出该产品的单价为m元，则他的满意度为
；如果他买进该产品的单价为n元，则他的满意度为
．如果一个人对两种交易（卖出或买进）的满意度分别为h1和h2，则他对这两种交易的综合满意度为
．现假设甲生产A、B两种产品的单件成本分别为12元和5元，乙生产A、B两种产品的单件成本分别为3元和20元，设产品A、B的单价分别为mA元和mB元，甲买进A与卖出B的综合满意度为h甲，乙卖出A与买进B的综合满意度为h乙
（1）求h甲和h乙关于mA、mB的表达式；当mA=
mB时，求证：h甲=h乙；
（2）设mA=
mB，当mA、mB分别为多少时，甲、乙两人的综合满意度均最大？最大的综合满意度为多少？
（3）记（2）中最大的综合满意度为h0，试问能否适当选取mA，mB的值，使得h甲≥h0和h乙≥h0同时成立，但等号不同时成立？试说明理由． 查看习题详情和答案>>
| m |
| m+a |
| a |
| n+a |
| h1h2 |
（1）求h甲和h乙关于mA、mB的表达式；当mA=
| 3 |
| 5 |
（2）设mA=
| 3 |
| 5 |
（3）记（2）中最大的综合满意度为h0，试问能否适当选取mA，mB的值，使得h甲≥h0和h乙≥h0同时成立，但等号不同时成立？试说明理由． 查看习题详情和答案>>
(其中
) ,
从左到右依次是函数
图象上三点,且
.
在
上是减函数；
是钝角三角形;