摘要：18． 在棱长为1的正方体ABCD-A′B′C′D′中.AC′为对角线.M.N分别为BB′.B′C′中点.P为线段MN中点. (1)求DP和平面ABCD所成的角的正切, (2)求四面体P-AC′D′的体积, (3)求DP和AC′所成角. 解:(1)过P作PH⊥BC于足H.连DH. ∵面BC′⊥面AC.则PH⊥面ABCD. ∴DP和面ABCD所成角即为∠HDP. 在正方形BCC′B′.M.N分别为BB′.B′C′中点.P为MN中点 (2)连BC′和B′C交于Q.因为BCC′B′为正方形.则PQ⊥BC′ (3)延长BC至E.延长至F.使CE=C′F=1.连DF.则DF//AC′ ∴异面直线AC′和DP所成角转化为求∠PDF.连PF
网址：http://m.1010jiajiao.com/timu3_id_4464145[举报]
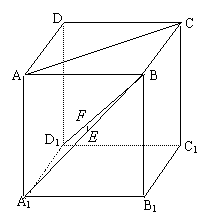在棱长为1的正方体
中，
为
上的点，且满足
，
为
上的点，且满足
。
与AC所成的角的大小;
∥平面
中，棱长
.
为棱
的中点，求证：
；
的大小；
到平面
的距离.
中，棱长
.
为棱
的中点，求证：
；
的大小；
到平面
的距离.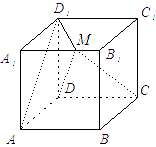
(本小题满分12分)
如图, 正方体ABCD－A1B1C1D1的棱长为6, 动点M在棱A1B1上. (1) 当M为A1B1的中点时, 求CM与平面DC1所成角的正弦值;
A1B1时, 求点C到平面D1DM的距离.