摘要:20. 设是定义在区间上的函数.且满足条件: (i) (ii)对任意的 (Ⅰ)证明:对任意的 (Ⅱ)判断函数是否满足题设条件, (Ⅲ)在区间[-1.1]上是否存在满足题设条件的函数.且使得对任意的 若存在.请举一例:若不存在.请说明理由. 绝密★启用前 普通高等学校招生全国统一考试
网址:http://m.1010jiajiao.com/timu3_id_4463667[举报]
(本小题满分14分)
设 是定义在
是定义在 上的函数,用分点
上的函数,用分点
将区间 任意划分成
任意划分成 个小区间,如果存在一个常数
个小区间,如果存在一个常数 ,使得和式
,使得和式 (
( )恒成立,则称
)恒成立,则称 为
为 上的有界变差函数.
上的有界变差函数.
(1)函数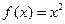 在
在 上是否为有界变差函数?请说明理由;
上是否为有界变差函数?请说明理由;
(2)设函数 是
是 上的单调递减函数,证明:
上的单调递减函数,证明: 为
为 上的有界变差函数;
上的有界变差函数;
(3)若定义在 上的函数
上的函数 满足:存在常数
满足:存在常数 ,使得对于任意的
,使得对于任意的 、
、 时,
时, .证明:
.证明: 为
为 上的有界变差函数.
上的有界变差函数.
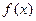 是定义在区间
是定义在区间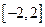 上的偶函数,命题
上的偶函数,命题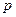 :
: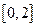 上单调递减;命题
上单调递减;命题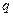 :
: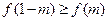 ,若“
,若“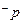 或
或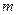 的取值范围。
的取值范围。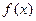 是定义在
是定义在 上的函数,用分点
上的函数,用分点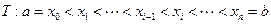
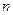 个小区间,如果存在一个常数
个小区间,如果存在一个常数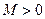 ,使得和式
,使得和式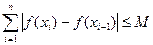 (
(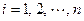 )恒成立,则称
)恒成立,则称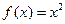 在
在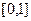 上是否为有界变差函数?请说明理由;
上是否为有界变差函数?请说明理由;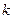 ,使得对于任意的
,使得对于任意的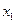 、
、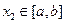 时,
时,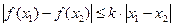 .证明:
.证明: