摘要:设是由函数上任意两点连线的斜率组成的集合.试写出是区间的一个函数. 填空选择专项训练(6)答卷纸 班级 姓名
网址:http://m.1010jiajiao.com/timu3_id_4463091[举报]
已知函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() .
.
(Ⅰ)求实数![]() 的值;
的值;
(Ⅱ)求函数![]() 在区间
在区间![]() 的最大值;
的最大值;
(Ⅲ)设![]() ,问是否存在实数
,问是否存在实数![]() ,使得函数
,使得函数![]() 的图象上任意不同的两点
的图象上任意不同的两点![]() 连线的斜率都大于
连线的斜率都大于![]() ?若存在,求出
?若存在,求出![]() 的取值范围;若不存在,说明理由.(
的取值范围;若不存在,说明理由.(![]() 为自然对数的底数,
为自然对数的底数,![]() )
)
已知函数f(x)=x+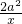 +alnx.
+alnx.
(I)求f(x)的单调递增区间;
(II)设a=1,g(x)=f′(x),问是否存在实数k,使得函数g(x)(均的图象上任意不同两点连线的斜率都不小于k?若存在,求k的取值范围;若不存在,说明理由.
查看习题详情和答案>>
已知函数f(x)=x+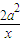 +alnx.
+alnx.
(I)求f(x)的单调递增区间;
(II)设a=1,g(x)=f′(x),问是否存在实数k,使得函数g(x)(均的图象上任意不同两点连线的斜率都不小于k?若存在,求k的取值范围;若不存在,说明理由.
查看习题详情和答案>>
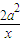 +alnx.
+alnx.(I)求f(x)的单调递增区间;
(II)设a=1,g(x)=f′(x),问是否存在实数k,使得函数g(x)(均的图象上任意不同两点连线的斜率都不小于k?若存在,求k的取值范围;若不存在,说明理由.
查看习题详情和答案>>
已知函数f(x)=x+
+alnx.
(I)求f(x)的单调递增区间;
(II)设a=1,g(x)=f′(x),问是否存在实数k,使得函数g(x)(均的图象上任意不同两点连线的斜率都不小于k?若存在,求k的取值范围;若不存在,说明理由. 查看习题详情和答案>>
| 2a2 | x |
(I)求f(x)的单调递增区间;
(II)设a=1,g(x)=f′(x),问是否存在实数k,使得函数g(x)(均的图象上任意不同两点连线的斜率都不小于k?若存在,求k的取值范围;若不存在,说明理由. 查看习题详情和答案>>
(2009•大连二模)(I)已知函数f(x)=x-
,x∈(
,
),P(x1,f(x1)),Q(x2,f(x2))是f(x)图象上的任意两点,且x1<x2.
①求直线PQ的斜率kPQ的取值范围及f(x)图象上任一点切线的斜率k的取值范围;
②由①你得到的结论是:若函数f(x)在[a,b]上有导函数f′(x),且f(a)、f(b)存在,则在(a,b)内至少存在一点ξ,使得f′(ξ)=
成立(用a,b,f(a),f(b)表示,只写出结论,不必证明)
(II)设函数g(x)的导函数为g′(x),且g′(x)为单调递减函数,g(0)=0.试运用你在②中得到的结论证明:
当x∈(0,1)时,f(1)x<g(x).
查看习题详情和答案>>
| 1 |
| x |
| 1 |
| 4 |
| 1 |
| 2 |
①求直线PQ的斜率kPQ的取值范围及f(x)图象上任一点切线的斜率k的取值范围;
②由①你得到的结论是:若函数f(x)在[a,b]上有导函数f′(x),且f(a)、f(b)存在,则在(a,b)内至少存在一点ξ,使得f′(ξ)=
| f(b)-f(a) |
| b-a |
| f(b)-f(a) |
| b-a |
(II)设函数g(x)的导函数为g′(x),且g′(x)为单调递减函数,g(0)=0.试运用你在②中得到的结论证明:
当x∈(0,1)时,f(1)x<g(x).