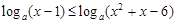摘要:解关于x的不等式:(且). 已知正项数列的前n项和.求的通项公式. 已知.直线l1:y=kx.l2:y=-kx. (Ⅰ)证明:到l1.l2的距离的平方和为定值a(a>0)的点的轨迹是圆或椭圆 (Ⅱ)求到l1.l2的距离之和为定值c(c>0)的点的轨迹. 已知三棱柱ABC-A1B1C1中.底面边长和侧棱长均为a.侧面A1ACC1⊥底面ABC.A1B=a. (Ⅰ)求异面直线AC与BC1所成角的余弦值, (Ⅱ)求证:A1B⊥面AB1C. 已知盒中有10个灯泡.其中8个正品.2个次品.现需要从中取出2个正品.每次取出1个.取出后不放回.直到取出2个正品为止.设ξ为取出的次品.求ξ的分布列及Eξ. 已知抛物线C:.过C上一点M.且与M处的切线垂直的直线称为C在点M的法线. (Ⅰ)若C在点M的法线的斜率为-.求点M的坐标(x0.y0), (Ⅱ)设P(-2.a)为C对称轴上的一点.在C上是否存在点.使得C在该点的法线通过点P?若有.求出这些点.以及C在这些点的法线方程,若没有.请说明理由.
网址:http://m.1010jiajiao.com/timu3_id_4462980[举报]
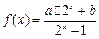 的反函数
的反函数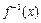 的图象过点
的图象过点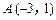 .
. 的值;
的值;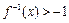
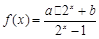 的反函数
的反函数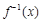 的图象过点
的图象过点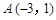 .
.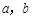 的值;
的值; 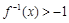
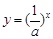 ,当
,当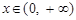 时,有
时,有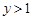 ,解关于x的不等式
,解关于x的不等式 。
。 ,当
,当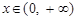 时,有
时,有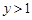 ,解关于x的不等式
,解关于x的不等式