摘要：解:(1)设B.C的坐标分别为 B(t,0),C(t-2,0), 则线段BC的中垂线方程为x=t-1, ① 1分 AB中点(,),AB斜率为(t≠0), 所以线段AB的中垂线方程为 y-= (x-) ② 3分 由①②得:x2=6y-8(-2≤x≤2且x≠-1) ③ 5分 当x=-1时.t=0时.三角形外心P为(-1,),适合③, 所以P点的轨迹为x2=6y-8 6分 (2)由得x2-2x-6b+8=0 ④ x1+x2=2,x1x2=8-6b 8分 所以|EF|==, 又因为d=, 11分 所以= = 13分 因方程④有两个不相同的实数根.设f(x)=x2-2x-6b+8 由题意(-2)2-4(8-6b)＞0得b＞,∴＜. 13分 当=时.即b=时.()max=. 所以的最大值是,此时b=. 14分
网址：http://m.1010jiajiao.com/timu3_id_4462097[举报]
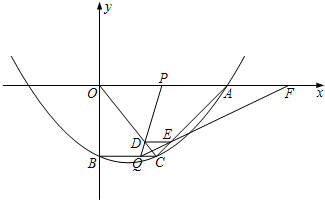如图，在平面直角坐标系xoy中，抛物线y=| 1 |
| 18 |
| 4 |
| 9 |
（1）求A，B，C三点的坐标和抛物线的顶点坐标；
（2）当t为何值时，四边形PQCA为平行四边形？请写出计算过程；
（3）当t∈（0，
| 9 |
| 4 |
（4）当t为何值时，△PQF为等腰三角形？请写出解答过程． 查看习题详情和答案>>
已知点P在曲线C：y＝
(x＞1)上，设曲线C在点P处的切线为l，若l与函数y＝kx(k＞0)的图像交于点A，与X轴相交于B点，设点P的横坐标为t，设A，B的横坐标分别为xA，xB，记f(t)＝xA·xB
(1)求函数f(t)的解析式
(2)设数列{an}(n≥1，n∈N)满足a1＝1，an＝f(
)(n≥2)，设数列{bn}(n≥1，n∈N，满足bn＝
－
，求{an}和{bn}的通项公式
(3)在(2)的条件下，当1＜k＜3时，证明不等式a1＋a2＋a3…＋an＞
．
已知点P在曲线
上，曲线C在点P的切线与函数y＝kx(k＞0)的图像交于点A，与x轴交于点B，设点P的横坐标为t，设A、B的横坐标分别为xA、xB，记f(t)＝xA·xB．
(1)求f(t)的解析式；
(2)设数列{an}(n≥1，n∈N)满足a1＝1，an＝f(
)(n≥2)，求数列{an}的通项公式；
(3)在(2)的条件下，当1＜k＜3时，证明不等式：a1＋a2＋a3…an＞
．
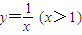上，曲线C在点P处的切线与函数y=kx（k＞0）的图象交于点A，与x轴交于点B，设点P的横坐标为t，点A、B的横坐标分别为xA、xB，记f（t）=xA•xB．
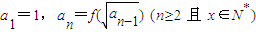，求数列{an}的通项公式；
．
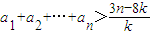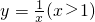上，曲线C在点P处的切线与函数y=kx（k＞0）的图象交于点A，与x轴交于点B，设点P的横坐标为t，点A、B的横坐标分别为xA、xB，记f（t）=xA•xB．
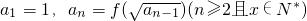，求数列{an}的通项公式；
．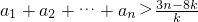