摘要:21. 如图.已知在坐标平面内.M.N是x轴上关于原点O对称的两点.P是上半平面内一点.△PMN的面积为 (Ⅰ)求以M.N为焦点且过点P的椭圆方程, 的直线l交椭圆于C.D两点.交直线x=-4于点E.点B.E分 ..求证:.
网址:http://m.1010jiajiao.com/timu3_id_4461528[举报]
(本小题满分12分)
如图,已知椭圆C1的中心在圆点O,长轴左、右端点M、N在x轴上,椭圆C1的短轴为MN,且C1,C2的离心率都为e,直线l⊥MN,l与C1交 于两点,与C1交于两点,这四点按纵坐标从大到小依次为A、B、C、D.
于两点,与C1交于两点,这四点按纵坐标从大到小依次为A、B、C、D.
(I)设e=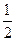 ,求|BC|与|AD|的比值;
,求|BC|与|AD|的比值;
(II)当e变化时,是否存在直线l,使得BO//AN,并说明理由.
(本小题满分12分)
如图,已知椭圆C1的中心在圆点O,长轴左、右端点M、N在x轴上,椭圆C1的短轴为MN,且C1,C2的离心率都为e,直线l⊥MN,l与C1交于两点,与C1交于两点,这四点按纵坐标从大到小依次为A、B、C、D.

(I)设e= ,求|BC|与|AD|的比值;
,求|BC|与|AD|的比值;
(II)当e变化时,是否存在直线l,使得BO//AN,并说明理由.
查看习题详情和答案>>
(本小题满分12分)
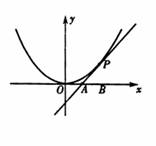 如图,已知直线l与抛物线
如图,已知直线l与抛物线![]() 相切于点P(2,1),且与x轴交于点A,O为坐标原点,定点B的坐标为(2,0).
相切于点P(2,1),且与x轴交于点A,O为坐标原点,定点B的坐标为(2,0).
(I) 若动点M满足![]() ,求点M的轨迹C;
,求点M的轨迹C;
(II)若过点B的直线l′(斜率不等于零)与(I)中的轨迹C交于不同的两点E、F(E在B、F之间),试求△OBE与△OBF面积之比的取值范围.
查看习题详情和答案>> 于两点,与C1交于两点,这四点按纵坐标从大到小依次为A、B、C、D.
于两点,与C1交于两点,这四点按纵坐标从大到小依次为A、B、C、D.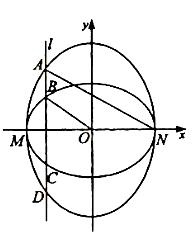
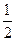 ,求|BC|与|AD|的比值;
,求|BC|与|AD|的比值; 当△PF1F2的边长恰好是三个连续的自然数时,求抛物线方程;此时设⊙C1、⊙C2……⊙Cn是圆心在
当△PF1F2的边长恰好是三个连续的自然数时,求抛物线方程;此时设⊙C1、⊙C2……⊙Cn是圆心在