摘要:已知函数 (1)判断函数的单调性,并用定义证明; (2)求函数的最大值和最小值. 若函数的最大值为.最小值为.求函数的单调区间和周期. 设函数f(x)对任意x.y∈R.都有f,且x>0时.f(x)<0. 为奇函数, 在R上为减函数. 已知函数 (I)求函数的最小正周期和单调增区间, (II)函数的图象可以由函数的图象经过怎样的变换得到? 某租赁公司拥有汽车100辆.当每辆汽车的月租金为3000元时.可全部租出.当每辆车的月租金每增加50元时.未租出的车辆会增加一辆.租出的车每辆每月需要维护费150元.未租出的车每辆每月需要维护费50元. (1)当每辆车的月租金定为3600元时.能租出多少辆车? (2)当每辆车的月租金定为多少元时.租赁公司的月收益最大?最大月收益是多少? 设函数. (1)在区间上画出函数的图像, (2)设集合. 试判断集合和之间的关系.并给出证明, (3)当时.求证:在区间上.的图像位于函数图像的上方.
网址:http://m.1010jiajiao.com/timu3_id_4458338[举报]

 的定义域与值域;
的定义域与值域;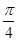 ,
,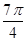 ]上的简图;
]上的简图;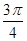 ]上的单调递增区间;试问:当x在R上取何值
]上的单调递增区间;试问:当x在R上取何值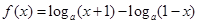 ,
,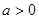 且
且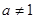 .
.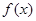 的定义域;
的定义域;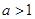 时,求使
时,求使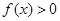 的
的 的取值范围.
的取值范围.