摘要:已知f(x)在上有定义.f()=-1.且满足x.y∈有f(x)+f(y)=f() ⑴证明:f(x)在上为奇函数, ⑵对数列x1=.xn+1=.求f(xn); ⑶求证 (Ⅰ)证明:令x=y=0.∴2f(0)=f(0).∴f(0)=0 令y=-x.则f(x)+f(-x)=f(0)=0 ∴f(x)+f(-x)=0 ∴f(-x)=-f(x) ∴f(x)为奇函数 4分 (Ⅱ)解:f(x1)=f()=-1.f(xn+1)=f()=f()=f(xn)+f(xn)=2f(xn) ∴=2即{f(xn)}是以-1为首项.2为公比的等比数列 ∴f(xn)=-2n-1 (Ⅲ)解: 而 ∴
网址:http://m.1010jiajiao.com/timu3_id_4454798[举报]
已知f(x)在(-1,1)上有定义,f(![]() )=-1,且满足x,y∈(-1,1)有f(x)+f(y)=f(
)=-1,且满足x,y∈(-1,1)有f(x)+f(y)=f(![]() )
)
⑴证明:f(x)在(-1,1)上为奇函数;?
⑵对数列x1=![]() ,xn+1=
,xn+1=![]() ,求f(xn);?
,求f(xn);?
⑶求证![]()
已知f(x)在(-1,1)上有定义,f(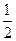 )=-1,且满足x,y∈(-1,1)有f(x)+f(y)=f(
)=-1,且满足x,y∈(-1,1)有f(x)+f(y)=f(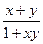 )
)
⑴证明:f(x)在(-1,1)上为奇函数;?
⑵对数列x1=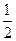 ,xn+1=
,xn+1= ,求f(xn);?
,求f(xn);?
⑶求证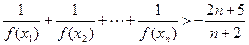
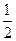 )=-1,且满足x,y∈(-1,1)有f(x)+f(y)=f(
)=-1,且满足x,y∈(-1,1)有f(x)+f(y)=f(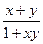 )
)⑴证明:f(x)在(-1,1)上为奇函数;?
⑵对数列x1=
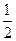 ,xn+1=
,xn+1= ,求f(xn);?
,求f(xn);?⑶求证
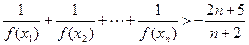
已知f(x)在(-1,1)上有定义,f(![]() )=-1,且满足x,y∈(-1,1)有f(x)+f(y)=f(
)=-1,且满足x,y∈(-1,1)有f(x)+f(y)=f(![]() ),
),
(1)判断f(x)在(-1,1)上的奇偶性;
(2)对数列x1=![]() ,xn+1=
,xn+1=![]() ,求f(xn).
,求f(xn).
(3)求证:![]() .
.
