摘要：设两条异面直线所成的角为q.则角q的范围 (A)00<q<1800 (B)00£q£900 (C)00<q£900 (D)00£q<900翰林汇
网址：http://m.1010jiajiao.com/timu3_id_4453685[举报]
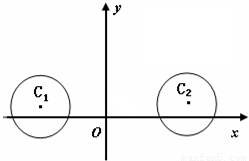
在平面直角坐标系xOy中，已知⊙C1：（x+3）2+（y-1）2=4和⊙C2：（x-5）2+（y-1）2=4（1）若直线l过点O（0，0），且被⊙C1截得的弦长为2
| 3 |
（2）设P为平面上的点，满足：过点P的任意互相垂直的直线l1和l2，只要l1和l2与⊙C1和⊙C2分别相交，必有直线l1被⊙C1截得的弦长与直线l2被⊙C2截得的弦长相等，试求所有满足条件的点P的坐标；
（3）将（2）的直线l1和l2互相垂直改为直线l1和l2所成的角为60°，其余条件不变，直接写出所有这样的点P的坐标．（直线与直线所成的角与两条异面直线所成的角类似，只取较小的角度．）
（本题满分14分） 在平面直角坐标系
中，已知⊙
：
和⊙
：
⑴若直线
过点
，且被⊙截得的弦长为
，求直线
的方程；
⑵设
为平面上的点，满足：过点的任意互相垂直的直线
和
，只要和与⊙和⊙分别相交，必有直线被⊙截得的弦长与直线被⊙截得的弦长相等，试求所有满足条件的点的坐标；
⑶将⑵的直线和互相垂直改为直线和所成的角为
，其余条件不变，直接写出所有这样的点的坐标。（直线与直线所成的角与两条异面直线所成的角类似，只取较小的角度。）
在平面直角坐标系xOy中，已知⊙C1：（x+3）2+（y-1）2=4和⊙C2：（x-5）2+（y-1）2=4
（1）若直线l过点O（0，0），且被⊙C1截得的弦长为
，求直线l的方程；
（2）设P为平面上的点，满足：过点P的任意互相垂直的直线l1和l2，只要l1和l2与⊙C1和⊙C2分别相交，必有直线l1被⊙C1截得的弦长与直线l2被⊙C2截得的弦长相等，试求所有满足条件的点P的坐标；
（3）将（2）的直线l1和l2互相垂直改为直线l1和l2所成的角为60°，其余条件不变，直接写出所有这样的点P的坐标．（直线与直线所成的角与两条异面直线所成的角类似，只取较小的角度．）
查看习题详情和答案>>
（1）若直线l过点O（0，0），且被⊙C1截得的弦长为
，求直线l的方程；（2）设P为平面上的点，满足：过点P的任意互相垂直的直线l1和l2，只要l1和l2与⊙C1和⊙C2分别相交，必有直线l1被⊙C1截得的弦长与直线l2被⊙C2截得的弦长相等，试求所有满足条件的点P的坐标；
（3）将（2）的直线l1和l2互相垂直改为直线l1和l2所成的角为60°，其余条件不变，直接写出所有这样的点P的坐标．（直线与直线所成的角与两条异面直线所成的角类似，只取较小的角度．）
查看习题详情和答案>>
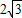，求直线l的方程；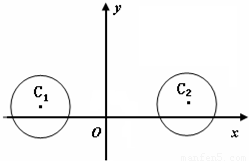
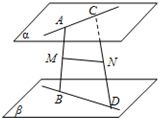设平面α∥β，两条异面直线AC和BD分别在平面α、β内，线段AB、CD中点分别为M、N，设MN=a，线段AC=BD=2a，求异面直线AC和BD所成的角．