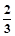摘要:设x1<x2-<xn,n∈N且n≥2.{x|(x-x1)(x-x2)-(x-xn)>0}{x|x2-(x1+xn)x+x1xn>0}.则n( ) A.等于2 B.是大于2的任意奇数 C.是大于2的任意偶数 D.是大于1的任意自然数
网址:http://m.1010jiajiao.com/timu3_id_4452894[举报]
设函数f(x)=-![]() x3+x2+(a2-1)x,其中a>0.
x3+x2+(a2-1)x,其中a>0.
(1)若函数y=f(x)在x=-1处取得极值,求a的值;
(2)已知函数f(x)有3个不同的零点,分别为0、x1、x2,且x1<x2,若对任意的x∈[x1,x2],f(x)>f(1)恒成立,求a的取值范围.
查看习题详情和答案>>(本小题满分14分)已知定义在实数集上的函数fn(x)=xn,n∈N*,其导函数记为 ,且满足
,且满足
 ,a,x1,x2为常数,x1≠x2.
,a,x1,x2为常数,x1≠x2.
(1)试求a的值;
(2)记函数
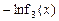 ,x∈(0,e],若F(x)的最小值为6,求实数b的值;
,x∈(0,e],若F(x)的最小值为6,求实数b的值;
(3)对于(2)中的b,设函数 ,A(x1,y1),B(x2,y2)(x1<x2)是函数g(x)图象上两点,若
,A(x1,y1),B(x2,y2)(x1<x2)是函数g(x)图象上两点,若 ,试判断x0,x1,x2的大小,并加以证明.
,试判断x0,x1,x2的大小,并加以证明.
(09年莱阳一中学段检测)(14分)
已知函数![]() ,
,![]() (a>0且a
(a>0且a![]() 1),其中
1),其中![]() 为常数.如果
为常数.如果
h(x)=f(x)+g(x)是增函数,且h(x)的导函数h![]() (x)存在零点.
(x)存在零点.
(1)求a的值;
(2)设A(x1、y1)、B(x2、y2)(x1 < x2)是函数y=g(x)的图象上两点,![]()
(g![]() (x)为g(x)的导函数),证明:x1 < x0 < x2
(x)为g(x)的导函数),证明:x1 < x0 < x2
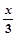 )=
)=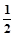 f(x);(3)f(1-x)=1-f(x),则f(
f(x);(3)f(1-x)=1-f(x),则f(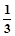 )+f(
)+f(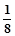 )=( )
)=( )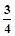 B.
B.