2008-2009学年度招远市第二学期初一第二学段测评
数学试题
说明:本试卷试题115分,书写质量3分,卷面安排2分,满分120分。
一、选择题(每小题2分,满分30分)
1.下列计算中,正确的是( )
A.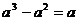 B.
B.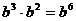
C.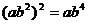 D.
D.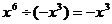
2.下列各数据中,精确的是( )
A.月球离地球约38万千米 B.田苗同学的体重约42千克
C.某校七年级2班有46名同学 D.今天气温约
3.如下图,直线 ,直线
,直线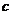 分别交
分别交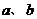 于点A和B,若∠2=4∠1,则∠2的度数为( )
于点A和B,若∠2=4∠1,则∠2的度数为( )
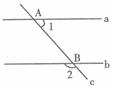
A.36° B.72° C.108° D.144°
4.计算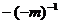 的结果为( )
的结果为( )
A.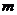 B.
B.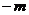 C.
C.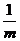 D.
D.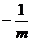
5.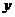 (元)和水果重
(元)和水果重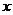 (千克)之间的关系是( )
(千克)之间的关系是( )
A.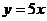 B.
B.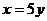 C.
C.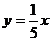 D.
D.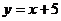
6.下列每组数分别是三根小木棒的长度,用它们不能摆成三角形的是( )
A.
C.
7.如下图,△ADE的顶点D在AABC的BC边上,且AD=AB,BC=DE,∠B=∠ADE,则下列结论不正确的是( )

A.∠C=∠E B.∠B=∠ADC
C.∠BAD=∠CAE D.∠CDE=∠CAE
8.用四舍五入法得到近似数0.4708,下列说法正确的是( )
A.精确到万位,有4个有效数字 B.精确到万分位,有4个有效数字
C.精确到万分位,有3个有效数字 D.精确到千分位,有4个有效数字
9.下图是个可以自由转动的转盘,转盘被分成6个全等的扇形,转动这个转盘,当它停止转动时,指针落在可能性最大的颜色区域是( )

A.绿色 B.红色 C.蓝色 D.黄色
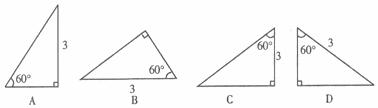
10.在△ABC中,∠C=90°,∠B=30°,BC=3,则下列四个直角三角形中,与△ABC全等的是( )
11.下图表示小王步行的路程与时间的关系,他在5小时内的平均速度是( )
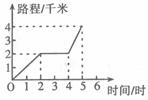
A.1.6千米ㄍ时 B.1.2千米ㄍ时 C.0.8千米ㄍ时 D.0.2千米ㄍ时
12.如下图,点D、E分别在∠BAC的边上,连接DC、BE,若∠B=∠C,那么补充下列一个条件后,仍无法判定△ABE≌△ACD的是( )
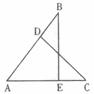
A.∠AEB=∠ADC B.AD=AE C.BE=CD D.AB=AC
13.如下图是5×5的正方形网格,以点D,E为顶点画格点三角形,使之与△ABC全等,这样的格点三角形最多可画出( )
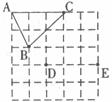
A.2个 B.4个 C.6个 D.8个
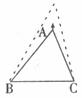
14.如下图,在△ABC中,BE边不动,点A竖直向上运动,∠A越来越小,∠B,∠C越来越大。若∠A减小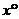 ,∠B增加
,∠B增加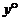 ,∠C增加
,∠C增加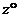 ,则
,则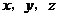 之间的关系是( )
之间的关系是( )
A.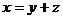 B.
B.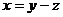
C.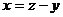 D.
D.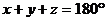
15.星期一早上,学校举行升国旗仪式,国旗距地面的高度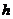 (米)与时间
(米)与时间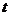 (秒)之间的关系用图像表示较为恰当的是( )
(秒)之间的关系用图像表示较为恰当的是( )

二、填空题(将正确答案填在横线上。每小题3分,满分30分)
16.一个氧原子的直径是
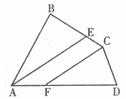
17.如下图,AE为∠BAD的平分线,CF为∠BCD的平分线,且AE∥CF,则∠B与∠D的关系为____________。
18.一盒子中装有10个白球和若干个其他颜色的球,盒中所有球除颜色不同外,其余都相同,从中任意摸出一球,若要使摸到白球的可能性比摸到不是白球的可能性大,则这个盒子里其他颜色的球最多有____________个。
19.等腰三角形的周长为12厘米,底边长为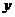 厘米,腰长为
厘米,腰长为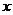 厘米。则y与x之间的关系式是____________。
厘米。则y与x之间的关系式是____________。
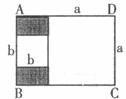
20.如下图,四边形ABCD是一个长方形,内有两个相邻的正方形,大、小正方形的边长分别为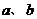 。则图中阴影部分的面积为____________。
。则图中阴影部分的面积为____________。
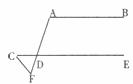
21.如下图,AB∥CE,AF交CE于D,连接CF,若∠C=37°,∠A=115°,那么∠F=____________度。
22.在△ABC中,若AB=8,BC=6,则第三边AC的长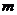 的取值范围是____________。
的取值范围是____________。
23.如下图,点D在BC上,AB⊥BC,EC⊥BC,AD⊥DE,且AD=DE,AB=3,EC=5,则BC的长为____________。

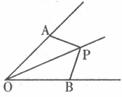
24.如下图,点P在∠AOB的平分线上,若使△AOP≌△BOP,则需要添加的一个条件是____________。(只写一个即可)
25.商店出售一种瓜子数量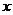 与售价
与售价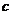 之间的关系如下表:
之间的关系如下表:
数量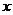 (克)
(克)
售价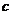 (元)
(元)
100
0.90+0.05
200
1.80+0.05
300
2.70+0.05
400
3.60+0.05
500
4.50+0 05
…
…
(表内售价栏中的0.05是塑料袋的价钱)
则用含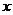 的代数式表示
的代数式表示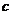 是____________。
是____________。
三、解答题(每小题6分,满分18分)
26.先化简,再求值:
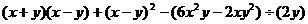 ,其中
,其中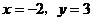
27.如下图是小明同学作的一周的零用钱开支的统计图(单位:元)。
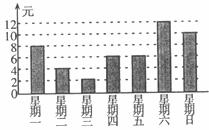
请根据图回答下列问题:
(1)星期几小明花的零用钱最少?是多少’
(2)哪几天他花的零用钱是一样的?分别为多少?
(3)请你帮小明算一算他一周平均每天花的零用钱(保留两个有效数字)
28.某工厂现在年产值是15万元,计划以后每年增加2万元,设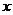 年后的年产值为
年后的年产值为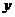 (万元)。
(万元)。
(1)写出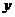 与
与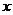 之间的关系式;
之间的关系式;
(2)用表格表示当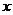 从0变化到5(每次增加1)
从0变化到5(每次增加1)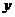 的对应值;
的对应值;
(3)求10年后的年产值;
四、尺规作图题(满分8分)
29.已知:线段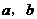 及
及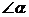 (如下图)。
(如下图)。
求作:△ABC,使∠A=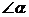 ,AB=
,AB=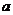 ,AC=
,AC=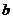 。
。
请你写出作法,作出相应的图形,保留作图痕迹。

五、探索题(满分9分)
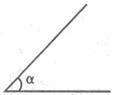
30.如下图,∠ACB=∠ADB=90°,AC=AD,点E在AB上。
(1)试说明点A在∠CBD的平分线上;
(2)请你探索线段CE与DE的数量关系,并说明理由。
六、实际应用题(每小题10分,满分20分)
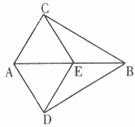
31.如下图①,要测量池塘两端A,B两点间的距离,小明的思路如图②所示,AC=CD,BC=CE,小颖的思路如图③所示,AC=CD。请你选择一种思路,先设计测量方案,再说明测量方案的合理性。
32.下面的图像表示一辆汽车的速度随时间变化而变化的情况。
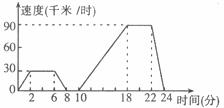
(1)汽车从出发到最后停止共经过了多少时间?它的最高时速是多少?
(2)汽车在哪段时间保持匀速行驶?时速是多少?
(3)汽车在哪段时间停止?可能发生了什么情况?
(4)请大致描述这辆汽车的行驶情况。