2008-2009学年度淄博博山初三义务教育课程实施水平反馈卷
数学试题
一、填空题
1.已知一元二次方程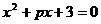 的一个根为-3,则p=__________.
的一个根为-3,则p=__________.
2.如图,∠BAC=∠ABD,请你添加一个条件:___________,使OC=OD(只添一个即可).
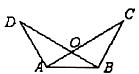
3.已知:如图,△OAD≌△OBC,且∠O=70°,∠C=25°,则∠AEB=__________度.
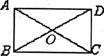
4.如图,在矩形ABCD中,对角线AC,BD交于点O,已知∠AOD=120°,AB=2.5,
则AC的长为___________.
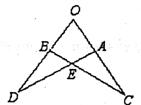
5.如图,在梯形ABCD中,AD//BC,E为BC上一点,DE∥AB,AD的长为1,BC的长为2,则CE的长为__________.
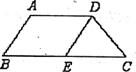
6.如图,△ABC中BE平分∠ABC,DE//BC,∠ABE=35°,则∠DEB=_______°,∠ADE=___________°.
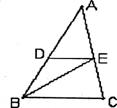
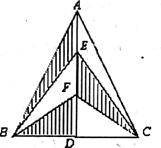
7.如图,AB=AC,∠BAC=120°,AB的垂直平分线交BC于点D,那么∠ADC= _________.
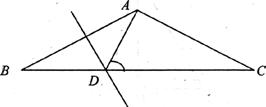
8.如图所示,菱形ABCD中,对角线AC,BD相交于点O,若再补充一个条件能使菱形ABCD成为正方形,则这个条件是__________(只填一个条件即可).
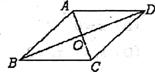
9.一种药品经过两次降价,药价从原来每盒60元降至现在的48.6元,则平均每次降价的百分率是___________.
10.如图,在四边形ABCD中,P是对角线BD的中点,E,F分别是AB,CD的中点,AD=BC,∠PEF=18°,则∠PFE的度数是___________.

11.如图,在△ABC中,AB=AC,AD是BC边上的高,点E、F是AD的三等分点,若△ABC的面积为l
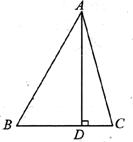
12.如图,在△ABC中,∠BAC=45°,AD⊥BC于D点,已知BD=6,CD=4,则高AD的长为__________.
二、选择题
1.方程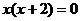 的根是 ( )
的根是 ( )
A.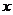 =2 B.
=2 B.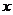 =0
=0
C.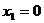 ,
,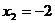 D.
D.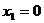 ,
,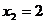
2.如果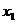 ,
,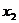 是一元二次方程
是一元二次方程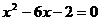 的两个实数根,那么
的两个实数根,那么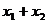 的值是 ( )
的值是 ( )
A.-6 B.-
3.若等腰三角形中有一个角等于50°,则这个等腰三角形的顶角的度数为 ( )
A.50° B.80° C.65°或50° D.50°或80°
4.如图,△ABC中,D,E分别是边AB,AC的中点,已知BC=10,则DE的长为( )
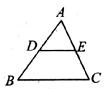
A.3 B.
5.若梯形的面积为8cm2,高为2cm,则此梯形的中位线长是 ( )
A.2cm B.4cm C.6cm D.8cm
6.如图,Rt△ABC中,AB⊥AC,AD⊥BC,BE平分∠ABC,交AD于E,EF//AC,下列结论一定成立的是( )

A.AB=BF B.AE=ED C.AD=DC D.∠ABE=∠DFE
7.如图,△ABC是等腰直角三角形,BC是斜边,将△ABP绕点A逆时针旋转后,能与△ACP'重合,如果AP=3,那么PP’的长等于 ( )
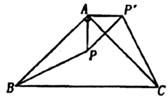
A.3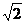 B.2
B.2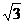 C.4
C.4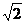 D.3
D.3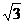
8.如图,将△ABC沿DE折叠,使点A与BC边的中点F重合,下列结论中:①EF//AB且EF=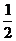 AB;②∠BAF=∠CAF;③S四边形ADFE=
AB;②∠BAF=∠CAF;③S四边形ADFE=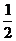 AF?DE;④∠BDF+∠FEC=2∠BAC,正确的个数是( )
AF?DE;④∠BDF+∠FEC=2∠BAC,正确的个数是( )
A.1 B.2 C.3 D.4
9.设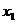 ,
,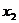 是关于
是关于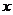 的一元二次方程
的一元二次方程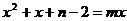 的两个实数根,且
的两个实数根,且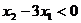 ,
,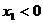 则 ( )
则 ( )
A.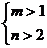 B.
B.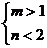 C.
C.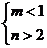 D.
D.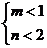
10.下列命题:
①若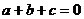 ,则
,则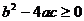 ;
;
②若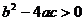 ,则一元二次方程
,则一元二次方程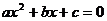 有两个不相等的实数根;
有两个不相等的实数根;
③若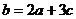 ,则一元二次方程
,则一元二次方程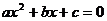 有两个不相等的实数根;
有两个不相等的实数根;
④若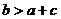 ,则一元二次方程
,则一元二次方程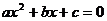 有两个不相等的实数根.
有两个不相等的实数根.
其中正确的是 ( )
A.只有①②③ B.只有①③④ C.只有①④ D.只有②③④
三、我们已经学习了一元二次方程的四种解法:因式分解法,开平方法,配方法和公式法.请从以下一元二次方程中任选一个,并选择你认为适当的方法解这个方程.
①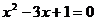 ;②
;② ;③
;③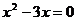 ;④
;④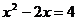 .
.
五、已知:如图,C为BE上一点,点A,D分别在BE两侧.AB//ED,AB=CE,BC=ED.求证:AC=CD.
四、如果-1是一元二次方程 的一个根,求它的另一根与
的一个根,求它的另一根与 的值.
的值.
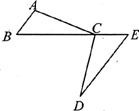
六、如图,正方形ABCD中,E与F分别是AD,BC上一点.在①AE=CF;②BE//DF;③∠l=∠2中,请选择其中一个条件,证明BE=DF.
(1)你选择的条件是________(只需填写序号);
(2)证明:

七、如图,这是一张等腰梯形纸片,它的上底长为2,下底长为4,腰长为2,这样的纸片共有5张.打算用其中的几张来拼成较大的等腰梯形,那么你能拼出哪几种不同的等腰梯形?分别画出它们的示意图,并写出它们的周长.

八、已知关于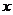 的方程
的方程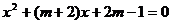 .
.
(1)求证方程有两个不相等的实数根.
(2)当m为何值时,方程的两根互为相反数?并求出此时方程的解.
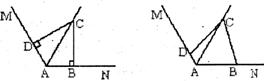
九、已知∠MAN,AC平分∠MAN.
(1)在图1中,若∠MAN=120°,∠ABC=∠ADC=90°,求证:AB+AD=AC;
(2)在图2中,若∠MAN=120°,∠ABC+∠ADC=180°,则(1)中的结论是否仍然成立?若成立,请给出证明:若不成立,请说明理由.
十、刚回营地的两个抢险分队又接到救灾命令:一分队立即出发赶往30千米外的A镇;二分队因疲劳可在营地休息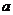 (0≤
(0≤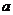 ≤3)小时再赶往A镇参加救灾。一分队出发后得知,唯一通往A镇的道路在离营地10千米处发生塌方,塌方处地形复杂,必须由一分队用1小时打通道路.已知一分队的行进速度为5千米/时,二分队的行进速度为(4+
≤3)小时再赶往A镇参加救灾。一分队出发后得知,唯一通往A镇的道路在离营地10千米处发生塌方,塌方处地形复杂,必须由一分队用1小时打通道路.已知一分队的行进速度为5千米/时,二分队的行进速度为(4+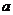 )千米/时.
)千米/时.
(1)若二分队在营地不休息,问二分队几个小时能赶到A镇?
(2)若需要二分队和一分队同时赶到A镇,二分队应在营地休息几个小时?