2008-2009学年度滕州市奎文北区第二学期七年级学业检测
数学试卷
说明:本试题满分120分,考试时间90分钟。
一、选择题:本大题共10小题,共40分。在每小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来。每小题选对得4分,选错、不选或选出的答案超过一个均记零分。
1.下列运算,正确的是
A.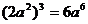 B.
B.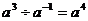
C.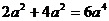 D.
D.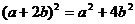
2.用科学记数法表示0.0625,应记作
A.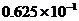 B.
B.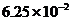 C.
C.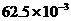 D.
D.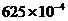
3.下列语句,叙述正确的是
A.近似数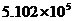 精确到千分位
精确到千分位
B.近似数0.001精确到百分位
C.近似数10.1万精确到千位,有三个有效数字
D.近似数210精确到个位,有一个有效数字
4.下列判断,错误的是
A.有两边和一角对应相等的两个三角形全等
B.有两角和一边对应相等的两个三角形全等
C.有一边对应相等的两个等边三角形全等
D.有两边和其中一边上的中线对应相等的两个三角形全等
5.变量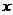 与
与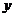 之间的关系是
之间的关系是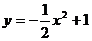 ,当自变量
,当自变量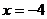 时,因变量
时,因变量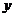 的值是
的值是
A.-1 B.
6.如下图,在四边形ABCD中,点E在BC上,AB∥DE,∠B=78°,∠C=60°,则∠EDC的度数为
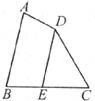
A.42° B.52° C.60° D.78°
7.口袋内装有一些除颜色外完全相同的红球、白球和黑球,从中摸出一球,摸出红球的概率是0.2,摸出自球的概率是0.5,那么摸出黑球的概率是
A.0.1 B.
8.如图,六边形ABCDEF是轴对称图形,CF所在的直线是它的对称轴,若∠AFC+∠BCF=150°,则∠AFE+∠BCD等于
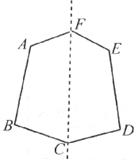
A.150° B.210° C.300° D.330°
9.如下图,三角形纸片ABC中,AB=10cm,BC=7cm,AC=6cm,沿过点B的直线折叠这个三角形,使顶点C落在AB边上的点E处,折痕为BD,则△AED的周长为

A.10cm B.9cm C.8cm D.7cm
10.如下图,点D,E分别在△ABC的边BC,AB上,且AD是CE的垂直平分线,AD交CE于F。下列结论:
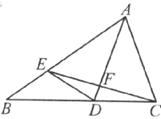
①AE=AC; ②DE=DC; ③AD平分∠BAC; ④AD与CE互相垂直平分。
其中,正确的结论有
A.4个 B.3个 C.2个 D.1个
二、填空题:本大题共6小题,每小题填对得4分,共24分。只要求填写最终结果。
11.计算: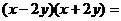 ____________。
____________。
12.已知∠A=43°,则∠A的余角为____________。
13.若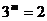 ,
,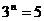 ,则
,则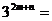 ____________。
____________。
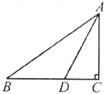
14.如下图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC于点D,CD=6,则点D到AB的距离是____________。
15.已知一个等腰三角形两内角的度数之比为1:4,则这个等腰三角形顶角的度数为____________。
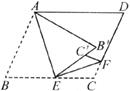
16.如下图,将一平行四边形纸片ABCD沿AE,EF折叠,使点B落在纸片ABCD内部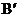 处,点C落在
处,点C落在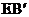 上
上 处,则∠AEF=____________。
处,则∠AEF=____________。
三、解答题:本大题共6小题,满分56分。
17.计算:(每小题5分,满分10分)
(1)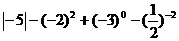
(2)
18.(本题满分8分)
要想测量河岸相对两点A、B的距离,先在AB的垂线BF上取两点C、D,使CD=BC,再定出BF的垂线DE,使A、C、E在一条直线上(如下图),因此,测得ED之长即为A、B的距离。以下是小英的想法,请你在括号内填上根据。
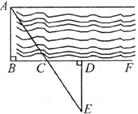
小英是这样想的:
因为AE和BD相交于点C,
所以∠ACB=∠ECD( )
又因为AB⊥BF,ED⊥BF,
所以∠ABC=∠EDC=90°( )
在△ABC和AEDC中,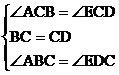
所以△ABC≌△EDC( )
所以ED=AB( )
19.(本题满分8分)
一口袋中装有5张完全相同的卡片,分别写有1cm、2cm、3cm、4cm和5cm,口袋外有2张卡片,分别写有4cm和5cm。现随机从口袋内取出一张卡片,与口袋外两张卡片放在一起,以卡片上的数量分别作为三条线段的长度组成三角形,回答下列问题:
(1)求这三条线段能构成三角形的概率;
(2)求这三条线段能构成等腰三角形的概率。
20.(本题满分10分)
某单位要印刷一批宣传资料,在需要支付制版费600元和每份资料0.3元印刷费的前提下,甲、乙两个印刷厂分别提出了不同的优惠条件。甲印刷厂提出:凡印刷数量超过2000份的,超过部分的印刷费可按9折收费;乙印刷厂提出:凡印刷数量超过3000份的,超过部分印刷费可按8折收费。
(1)如果该单位要印刷2400份宣传资料,那么甲印刷厂的费用是_________,乙印刷厂的费用是_________;
(2)设印刷数量为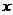 份,当
份,当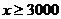 时,请分别写出甲、乙印刷厂的费用
时,请分别写出甲、乙印刷厂的费用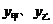 与
与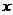 之间的关系式。
之间的关系式。
21.(本题满分10分)
如下图,一块三角形模具的阴影部分已破损。
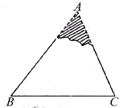
(1)从残留的模具片中度量出哪些边、角,就可以不带残留的模具片到店铺加工一块与原来的模具ABC的形状和大小完全相同的模具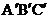 ?
?
(2)作出模具△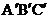 的图形。(尺规作图,保留作图痕迹,不写作法)
的图形。(尺规作图,保留作图痕迹,不写作法)
22.(本题满分10分)
小亮早晨从家骑车到学校,先上坡后下坡,行程情况如下图所示。
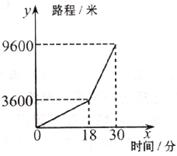
(1)求上坡、下坡的速度;
(2)若返回时上坡、下坡的速度仍保持不变,求小明从学校骑车回家用的时间。