2006-2007学年度济宁市微山县第二学期期末考试
八年级数学试题
一、精心选一选(本大题共12小题,每题3分,共36分。在每题所给出的四个选项中,只有一项是符合题意的。把所选项前的字母代号填在下表内。相信你一定能选对!)
1.下列方程是分式方程的是( )
A.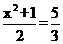 B.
B.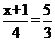
C.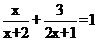 D.
D.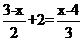
2.医学研究发现一种新病毒的直径约为0.000043毫米,则这个数用科学记数法表示为( )
A.0.43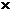 10
10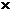
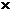 10
10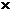
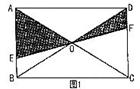
3.如图1,直线EF过矩形ABCD对角线的交点O,且分别交AB、CD于E、F两点,那么阴影部分的面积是矩形ABCD面积的( )
A.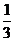 B.
B.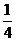 C.
C.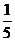 D.
D.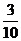
4.在直线L上依次摆放着七个正方形(如图2所示)。已知斜放置的三个正方形的面积分别是1、2,3,正放置的四个正方形的面积依次是S1、S2、S3、S4,则S1+S2+S3+S4= 。
A.3 B.
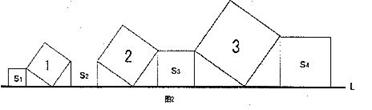
5.如图3,折叠长方形ABCD的一边AD,使点D落在BC边上的点F处,设折痕为AE,若AB=8,AD=10,则DE的值是( )
A.3 B.
6.刘翔出征2008年奥运会前刻苦进行
A.众数 B.方差 C.平均数 D.中位数
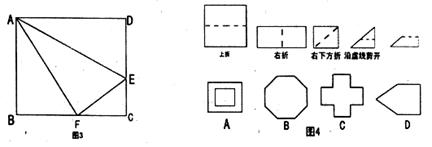
7.如图4所示,把一个正方形三次对折后沿虚线剪下,则展开后所得的图形是( )
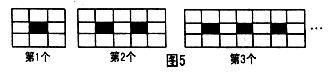
8.下列图案(图5)是由边长相等的黑白两色的正方形按一定规律拼接而成,依此规律,第5个图案中白色正方形的个数是( )
A.23 B.
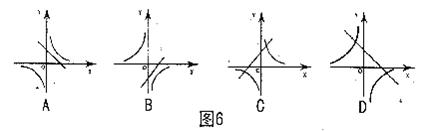
9.如图6,函数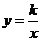 和
和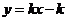 在同一坐标系中的图像大致是( )
在同一坐标系中的图像大致是( )
10.如图7,在矩形ABCD中,AB=3,AD=4,P是AD上的动点,PE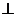 AC于E,PF
AC于E,PF BD于F,则PE+PF的值为( )
BD于F,则PE+PF的值为( )
A.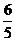 B.
B.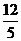 D.4
D.4

11.某闭合电路中,电压为定值,电流I(A)与电阻R( )成反比例,如图8表示的是该电路中电流I与电阻R的函数关系的图像,则用电阻R表示电流I的函数关系为( )
)成反比例,如图8表示的是该电路中电流I与电阻R的函数关系的图像,则用电阻R表示电流I的函数关系为( )
A.I= B.I=
B.I= C.I=
C.I=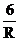 D.I=
D.I=
12.如图9所示,在等腰梯形ABCD中,AD//BC,AC,BD相交于点O,有如下五个结论:①AC=BD ② OBC=
OBC= OCB ③梯形ABCD是轴对称图形 ④
OCB ③梯形ABCD是轴对称图形 ④ AOB
AOB
 DOC ⑤
DOC ⑤ ABC=
ABC=  DCB,其中正确的有( )
DCB,其中正确的有( )
A.2个 B.3个 C.4个 D.5个
二、细心填一填(本大题共有6小题,每题3分,共18分。请把结果直接填在题中的横线上。只要你仔细运算,积极思考,相信你一定能填对!)
13.当x= 时,分式 没有意义。
没有意义。
14.平行四边形ABCD的周长为 AOB的周长比
AOB的周长比 BOC的周长多
BOC的周长多
15.已知:在梯形ABCD中,AD∥BC,CA平分 BCD,CD=5,则AD= 。
BCD,CD=5,则AD= 。
16.某公司销售部有5名销售员,2006年月平均销售额分别为6、8、11、9、8(万元),现公司要增加一名销售员,甲、乙、丙三人应聘,并试用三个月,平均每人每月的销售额分别是:甲是上述数据的平均数,乙是上述数据的中位数,丙是上述数据的众数,最后录用三人中平均销售额最高的人是 。
17.如图10,ABCD为菱形, AEF为正三角形,其中,E、F分别在BC、CD上,若三角形边长与菱形的边长相等,则
AEF为正三角形,其中,E、F分别在BC、CD上,若三角形边长与菱形的边长相等,则 BAD= 。
BAD= 。

18.如图11,图中所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长是
三、认真答一答(本大题共7题,满分66分。只要你认真审题,细心运算,一定能解答正确!)(解答应写出文字说明、证明过程或推演过程)
19.(1)(6分)请将下面的代数式尽可能化简,再选择一个你喜欢的数(要合适哦!)代入求值: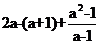
(2)(6分)解分式方程
(1)观察上述方程及解,猜想并求关于x的方程 上的解。
上的解。
(2)把关于x的方程 变为(1)中方程的形式,并求此方程的解。
变为(1)中方程的形式,并求此方程的解。
21.(8分)已知,如图12,E、F分别是平行四边形ABCD的AD、BC边上的点,且AE=CF
(1)求证: ABE
ABE
 CDF
CDF
(2)若M、N分别是BE、DF的中点,连接MF、EN,试判断四边形MFNE是怎样的四边形,并证明你的结论。

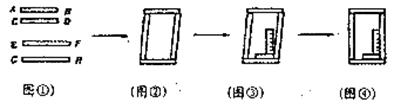
22.(6分)工人师傅做铝合金窗框分下面三个步骤进行:
(1)先截出两对符合规格的铝合金窗料(如图①),使AB=CD,EF=GH;
(2)摆放成如图②的四边形,则这时窗框的形状是 形,根据的数学道理是: 。
(3)将直角尺靠紧窗框的一个角(如图③),调整窗框的边框,当直角尺的两条直角边与窗框无缝隙时(如图④,说明窗框合格,这时窗框是 形,根据的数学道理是: 。
23.(12分)张老师为了从王军、张成两位同学中选拔一人参加“全国初中数学联赛”,对两位同学进行了辅导,并在辅导期间进行了10次测验,两位同学测验成绩记录如下表:
第1次
第2次
第3次
第4次
第5次
第6次
第7次
第8次
第9次
第10次
王军
68
80
78
79
81
77
78
84
83
92
张成
86
80
75
83
85
77
79
80
80
75
利用表中提供的数据,解答下列问题:
(1)填写完成下表:
平均成绩
中位数
众数
王军
79.5
张成
80
80
(2)张老师从测验成绩记录表中,求得王军10次测验成绩的方差S12=33.2,请你帮助张老师计算张成10次测验成绩的方差S22;
(3)请你根据上面的信息,运用所学的统计知识,帮助张老师做出选择,应派谁去参加联赛,并简要说明理由。
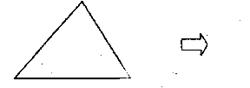
24.(8分)直角三角形通过剪切可以拼成一个与该直角三角形面积相等的矩形,方法如下:

请你用上面图示的方法,解答下列问题:
(1)对任意三角形,设计一种方案,将它分成若干块,再拼成一个与原三角形面积相等的矩形。
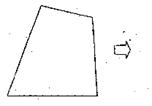
(2)对任意四边形,设计一种方案,将它分成若干块,再拼成一个与原四边形面积相等的矩形。
25.(12分)点P是x轴正半轴上的一个动点,过点P作x轴的垂线PA交双曲线 于点A,连结OA。
于点A,连结OA。
(1)如图①,当点P在x轴的正方向上运动时,Rt AOP的面积大小是否变化?若不变,请求出Rt
AOP的面积大小是否变化?若不变,请求出Rt AOP的面积;若改变,试说明理由。
AOP的面积;若改变,试说明理由。
(2)如图②,在x轴上点P的右侧有一点D,过点D作x轴的垂线交双曲线于点B,连结BO 交AP于点C。设 AOP的面积为S1,梯形BCPD的面积为S2,则S1与S2大小关系是S1 S2 (填“>”或“<”或“=”)。
AOP的面积为S1,梯形BCPD的面积为S2,则S1与S2大小关系是S1 S2 (填“>”或“<”或“=”)。
(3)如图③,AO的延长线与双曲线 的另一个交点为点F,FH垂直于x轴,垂足为点H,连结AH、PF,试证明四边形APFH的面积为一常数。
的另一个交点为点F,FH垂直于x轴,垂足为点H,连结AH、PF,试证明四边形APFH的面积为一常数。
