2007-2008学年度潍坊市高密上学期期末考试
八年级数学试题
(时间:90分钟 满分:120分)
一、选择题(共10个小题,每小题3分,共30分)
1.下列运算正确的是( )
(A)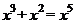 (B)
(B)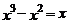 (C)
(C)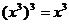 (D)
(D)
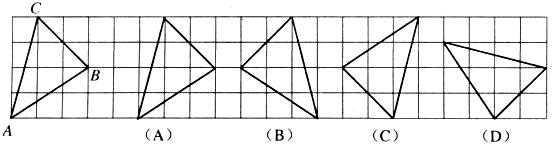
2.在下图右侧的四个三角形中,不能由△ABC经过旋转或平移得到的是( )
3.下列图案中,不是中心对称图形的是( )

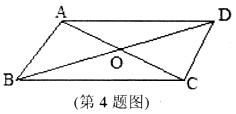
4.如图所示,在平行四边形ABCD中,对角线AC、BD交于点O,下列式子中一定成立的是( )
(A)AC⊥BD (B)AO=OD (C)AC=BD (D)OA=OC
5.下列四边形:①等腰梯形;②正方形;③矩形:④菱形中,对角线一定相等的是( )
(A)①②③ (B)①②③④ (C)①② (D)②③
6.下列判断中错误的是( )
(A)有两角和一边对应相等的两个三角形全等
(B)有两边和一角对应相等的两个三角形全等
(C)有两边和其中一边上的中线对应相等的两个三角形全等
(D)有一边对应相等的两个等边三角形全等
7.如图,在Rt△ACB中,∠C=90°,∠B=60°,将△ACB绕点A逆时针旋转70°后得到△AC′B′,则,∠CAB′为( )
(A)60° (B)70° (C)100° (D)120°

8.正方形具有而菱形不具有的性质是( )
(A)四个角都是直角 (B)内角和为360° (C)两组对边分别相等 (D)对角线平分对角
9.若等腰梯形两底之差等于一腰的长,则这个梯形的一个内角的度数为( )
(A)30° (B)45° (C)60° (D)75°
10.若 a、b、c是直角三角形的三条边长,斜边c上的高的长是h,给出下列结论
①以 ,
, ,
, 的长为边的三条线段能组成一个三角形
的长为边的三条线段能组成一个三角形
②以 ,
, ,
, 的长为边的三条线段能组成一个三角形
的长为边的三条线段能组成一个三角形
③以a+b,c+h,h的长为边的三条线段能组成直角三角形
④以 ,
, ,
, 的长为边的三条线段能组成直角三角形
的长为边的三条线段能组成直角三角形
其中所有正确结论个数有( )
(A)1个 (B)2个 (C)3个 (D)4个
二、填空题(共8个小题,每个小题3分,共24分)
11.图形在平移、旋转过程中有一个共同的特征,即图形的__________和_________不变.
12.计算: =____________.
=____________.
13.如图,若△OAD≌△OBC,且∠O=65°,∠C=20°,则∠OAD=____________.

14.已知平行四边形ABCD中,∠ABC的平分线交AD于点E,且AE=2,DE=1,则平行四边形ABCD的周长等于____________.
15.若 ,
, ,则
,则 =____________.
=____________.
16.已知等腰三角形ABC中AB=AC=
17.如图,AC、BD相交于点O,∠A=∠D,请你再补充一个条件,使得△AOB≌△DOC,你补充的条件是____________.
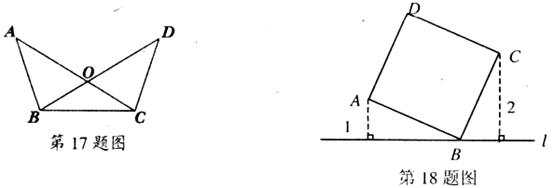
18.如图,直线 过正方形ABCD的顶点B,点A,C到直线
过正方形ABCD的顶点B,点A,C到直线 的距离分别是1和2,则正方形的边长是____________.
的距离分别是1和2,则正方形的边长是____________.
三、解答题(共8个小题,满分66分)
19.(本题满分6分)
先化简,再求值. ,其中
,其中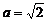 ,
,
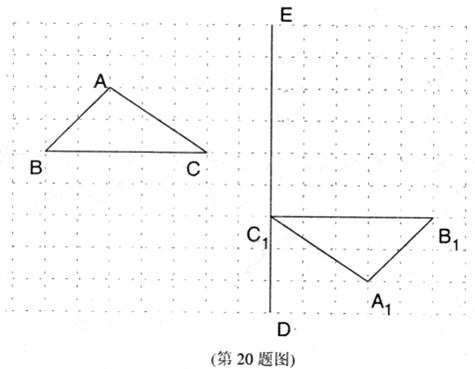
20.(本题满分9分).在如图的方格纸中,每个小正方形的边长都为1,△ABC与△A1B
(1)画出此中心对称图形的对称中心O:
(2)画出将△A1B
(3)要使△A2B
21.(本题满分6分)给出三个多项式: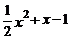 ,
,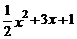 ,
,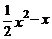 ,请你选择其中两个进行加法运算,并把结果因式分解.
,请你选择其中两个进行加法运算,并把结果因式分解.
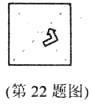
22.(本题满分8分)我们已经学过在平面内,如果一个图形绕一个定点旋转一定的角度后能与自身重合,那么就称这个图形是旋转对称图形,转动的这个角称为这个图形的一个旋转角。例如:正方形绕着它的对角线的交点旋转90°后能与自身重合(如图),所以正方形是旋转对称图形,它有一个旋转角为90°。
(1)判断下列命题的真假(在相应的括号内填上“真”或“假”)。
①等腰梯形是旋转对称图形,它有一个旋转角为180°.( )
②矩形是旋转对称图形,它有一个旋转角为180°.( )
(2)填空:下列图形中,是旋转对称图形,且有一个旋转角为120°的是_________________(写出所有正确结论的序号):①正三角形;②正方形;③正六边形;④正八边形。
(3)写出两个多边形,它们都是旋转对称图形,都有一个旋转角为72°,并且分别满足下列条件
①是轴对称图形,但不是中心对称图形:______________________________
②既是轴对称图形,又是中心对称图形:______________________________
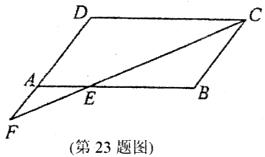
23.(本题满分8分)
已知:如图,平行四边形ABCD中,∠BCD的平分线交AB于E,交DA的延长线于F.
求证:AE=AF.
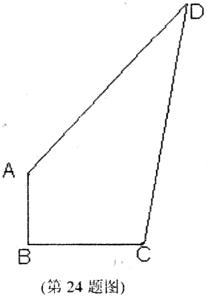
24.(本题满分8分)园丁住宅小区有一块草坪如图所示.已知,AB=
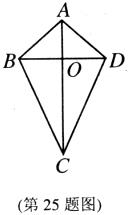
25.(本题满分10分)两组邻边分别相等的四边形我们称它为筝形.
如图,在筝形ABCD中,AB=AD,BC=DC,AC,BD相交于点O,
(1)求证:①△ABC≌△ADC;
②OB=OD,AC⊥BD;
(2)如果AC=6,BD=4,求筝形ABCD的面积
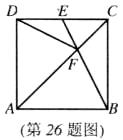
26.(本题满分11分)
如图,在正方形ABCD中,E是CD边的中点,AC与BE相交于点F,连接DF.
(1)在不增加点和线的前提下,直接写出图中所有的全等三角形;
(2)连接AE,试判断AE与DF的位置关系,并证明你的结论;
(3)延长DF交BC于点M,试判断BM与MC的数量关系.(直接写出结论)