2007年苏州市初中毕业暨升学考试试卷
数 学
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共三大题、29小题,满分125分;考试用时120分钟。
第Ⅰ卷(选择题,共27分)
一、选择题(本大题共9小题,每小题3分,共27分。在每小题给出的四个选项中,只有一个选项符合题意的。请将选择题的答案填在第Ⅱ卷前的《第Ⅰ卷答题表》内)
1.若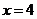 ,则
,则 的值是( )
的值是( )
A.1 B.-1 C.9 D.-9
2.若  ,则
,则 的值是( )
的值是( )
A.8 B.16 C.2 D.4
3.根据苏州市海关统计,
A.1.488×104 B.1.488×105 C.1.488×106 D.1.488×107
4.如图,MN为⊙O的弦,∠M=50°,则∠MON等于 ( )

A.50° B.55° C.65° D.80°
5.某同学7次上学途中所花时间(单位:分钟)分别为10,9,11,12,9,10,9。这组数的众数为 ( )
A.9 B.10 C.11 D.12
6.方程组 的解是 ( )
的解是 ( )
A. B.
B.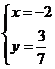 C.
C.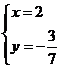 D.
D.
7.下列图形中,不能表示长方体平面展开图的是 ( )

8.下图是一个旋转对称图形,以O为旋转中心,以下列哪一个角为旋转角旋转,能使旋转后的图形与原图形重合( )

A.60° B.90° C.120° D.180°
9.如图,小明作出了边长为的第1个正△A1B

A. B.
B. C.
C. D.
D.
第Ⅱ卷(非选择题,共98分)
二、填空题:(本大题共8小题,每小题3分,共24分。把答案填在题中横线上。)
10. 的倒数是_______________
的倒数是_______________
11.9的算术平方根是_____________
12.一只口袋中放着8只红球和16只白球,现从口袋中随机摸一只球,则摸到白球的概率是___________
13.将抛物线 的图像向右平移3个单位,则平移后的抛物线的解析式为___________
的图像向右平移3个单位,则平移后的抛物线的解析式为___________
14.如图,已知扇形的半径为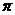 )
)

15.某校认真落实苏州市教育局出台的“三项规定”,校园生活丰富多彩.星期二下午4 点至5点,初二年级240名同学分别参加了美术、音乐和体育活动,其中参加体育活动人数是参加美术活动人数的3倍,参加音乐活动人数是参加美术活动人数的2倍,那么参加美术活动的同学其有____________名。
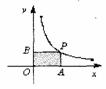
16.已知点P在函数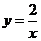 (x>0)的图象上,PA⊥x轴、PB⊥y轴,垂足分别为A、B,则矩形OAPB的面积为__________.
(x>0)的图象上,PA⊥x轴、PB⊥y轴,垂足分别为A、B,则矩形OAPB的面积为__________.
17.如图,将纸片△ABC沿DE折叠,点A落在点A′处,已知∠1+∠2=100°,则∠A的大小等于____________度.
(第18~20题,每题5分,共15分)
三、解答题:(本大题共12小题.共74分.解答时应写出必要的计算过程、推演步骤或文字说明.)
18.计算: .
.
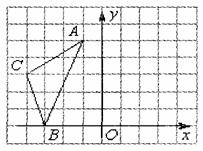
19.如图所示,在直角坐标系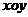 中,A(一l,5),B(一3,0),0(一4,3).
中,A(一l,5),B(一3,0),0(一4,3).
(1)在右图中作出△ABC关于y轴的轴对称图形△A′B′C′;
(2)写出点C关于,轴的对称点C′的坐标(_____,_______)。
20.解不等式组: .
.
(第21题5分.第22题6分.共11分)
21.如图,在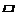 ABCD中,点E是AD的中点,BE的延长线与CD的延长线相交于点F
ABCD中,点E是AD的中点,BE的延长线与CD的延长线相交于点F
(1)求证:△ABE≌△DFE;
(2)试连结BD、AF,判断四边形ABDF的形状,并证明你的结论.
22.先化简,再求值: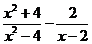 ,其中
,其中 .
.
(第23~24题,每题6分.共12分)
23.解方程: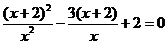 .
.
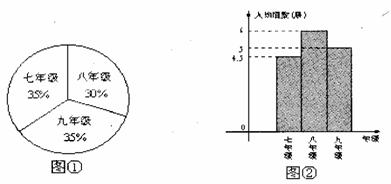
24.
根据以上信息解答下列问题:
(1)从图②中,我们可以看出人均捐赠图书最多的是_______年级;
(2)估计九年级共捐赠图书多少册?
(3)全校大约共捐赠图书多少册?
(第25题6分,第26题7分.共13分)
25.某学校体育场看台的侧面如图阴影部分所示,看台有四级高度相等的小台阶.已知看台高为l
(1)求点D与点C的高度差DH;
(2)求所用不锈钢材料的总长度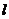 (即AD+AB+BC,结果精确到
(即AD+AB+BC,结果精确到
(参考数据:sin66.5°≈0.92,cos66.5°≈0.40,tan66.5°≈2.30)
26.小军与小玲共同发明了一种“字母棋”,进行比胜负的游戏.她们用四种字母做成10只棋子,其中A棋1只,B棋2只,C棋3只,D棋4只.
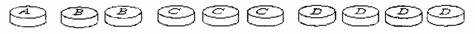
“字母棋”的游戏规则为:
①游戏时两人各摸一只棋进行比赛称一轮比赛,先摸者摸出的棋不放回;
②A棋胜B棋、C棋;B棋胜C棋、D棋;C棋胜D棋;D棋胜A棋;
③相同棋子不分胜负.
(1)若小玲先摸,问小玲摸到C棋的概率是多少?
(2)已知小玲先摸到了C棋,小军在剩余的9只棋中随机摸一只,问这一轮中小玲胜小军的概率是多少?
(3)已知小玲先摸一只棋,小军在剩余的9只棋中随机摸一只,问这一轮中小玲希望摸到哪种棋胜小军的概率最大?
(第27题7分)
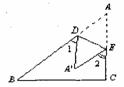
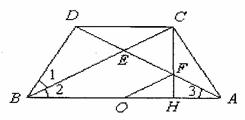
27.如图,已知AD与BC相交于E,∠1=∠2=∠3,BD=CD,∠ADB=90°,CH⊥AB于H,CH交AD于F.
(1)求证:CD∥AB;
(2)求证:△BDE≌△ACE;
(3)若O为AB中点,求证:OF=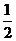 BE.
BE.
(第28题 8分)
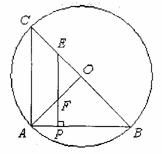
28.如图,BC是⊙O的直径,点A在圆上,且AB=AC=4.P为AB上一点,过P作PE⊥AB分别BC、OA于E、F
(1)设AP=1,求△OEF的面积.
(2)设AP=a (0<a<2),△APF、△OEF的面积分别记为S1、S2。
①若S1=S2,求a的值;
②若S= S1+S2,是否存在一个实数a,使S<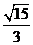 ?
?
若存在,求出一个a的值;若不存在,说明理由.
(第29题8分)
29.设抛物线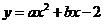 与x轴交于两个不同的点A(一1,0)、B(m,0),与y轴交于点C.且∠ACB=90°.
与x轴交于两个不同的点A(一1,0)、B(m,0),与y轴交于点C.且∠ACB=90°.
(1)求m的值和抛物线的解析式;
(2)已知点D(1,n )在抛物线上,过点A的直线 交抛物线于另一点E.若点P在x轴上,以点P、B、D为顶点的三角形与△AEB相似,求点P的坐标.
交抛物线于另一点E.若点P在x轴上,以点P、B、D为顶点的三角形与△AEB相似,求点P的坐标.
(3)在(2)的条件下,△BDP的外接圆半径等于________________.
