2007年临沂市中考模拟数学试题(二)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。第Ⅰ卷1至2页,第Ⅱ卷3至8页。满分l20分,考试时间120分钟。
第Ⅰ卷 (选择题 共42分)
注意事项:
1.答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上。
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案,不能答在试卷上。
3.考试结束,将本试卷和答题卡一并交回。
一、选择题(每小题3分。在给出的四个选项中,只有一项是符合题目要求的)
1.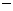 3的绝对值等于
3的绝对值等于
A.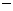 3 B.
3 B. D.
D.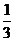
2.下列运算中,正确的是
A.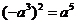 B.
B.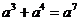
C.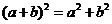 D.
D.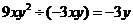
3.已知点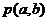 是平面直角坐标系中第四象限内的点,那么化简:
是平面直角坐标系中第四象限内的点,那么化简: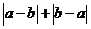 结果是
结果是
A.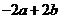 B.
B. C.
C.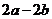 D.0
D.0
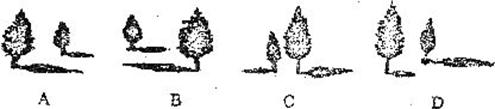
4.下列四幅圆形中,表示两棵树在同一对刻阳光下的影子的图形可能是
5.空气的体积质量是
A.1.239×10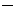 3 B.1.23×10
3 B.1.23×10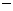 3
3
C.1.24×10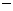 3 D.1.24×103
3 D.1.24×103
6.下图中几何体的左视图是
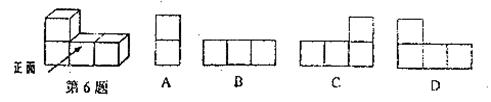
7.生活处处皆学问,如图,眼镜镜片所在的两圆的位置关系是
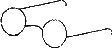
A.外离 B.外切 C.内含 D.内切
8.下列基本器形中,经过平移、旋转或轴对称变换后,不能得到下图的是

9.有两块面积相同的小麦试验田,分别收获小麦 kg,根据题意,可得方程
kg,根据题意,可得方程
A.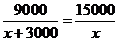 B.
B.
C.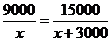 D.
D.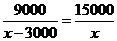
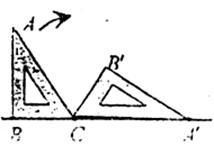
10.如下图,一块含有60°角的直角三角板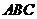 ,在水平桌面上绕点
,在水平桌面上绕点 按顺时针方向旋转到
按顺时针方向旋转到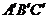 的位置,若
的位置,若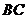 的长为
的长为 从开始到结束所经过的路径长为
从开始到结束所经过的路径长为
A. cm B.10
cm B.10
 cm C.15
cm C.15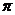 cm D.20
cm D.20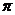 cm
cm
11.若一个圆锥的侧面积为20,则下列图像中表示这个圆锥的母线长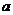 与底面半径
与底面半径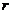 之间的函数关系的是
之间的函数关系的是
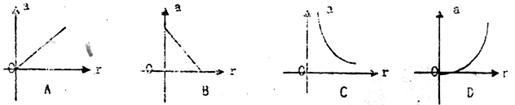
12.已知点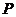 是半径为5的圆
是半径为5的圆 内一定点,且
内一定点,且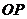 =4,则过点
=4,则过点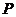 的所有弦中,弦长可能取的整数有( )个
的所有弦中,弦长可能取的整数有( )个
A.2 B.3 C.4 D.5
13.甲、乙两同学参加创建全国文明城市知识竞赛,共有l0道不同的题,其中选择题6个,判断题4个。甲、乙两人先后各抽一题(不放回),则甲抽到选择题的概率,乙抽到判断题的概率分别是
A.
 B.
B.
 C.
C.
 D.
D.

14.如下图是一声长方形 的场地,长
的场地,长 =102m,宽
=102m,宽 =51m,从
=51m,从 、
、 两处入口的中路宽都为1m。两小路汇合处路宽为2m,其余部分种植草坪,则草坪面积为
两处入口的中路宽都为1m。两小路汇合处路宽为2m,其余部分种植草坪,则草坪面积为

A.5050m2 B.4900m2 C.5000m2 D.4998m2
第Ⅱ卷 (非选择题 共78分)
二、填空题(本大题共5小题,每小题3分,共15分)。将答案写在对应题号的横线上。
15.如果我们规定 ,那么不等式
,那么不等式 的解集为
。
的解集为
。
16.如下图,A是硬币圆周上一点,硬币与数轴相切于原点 (
( 与
与 点重合)。假设硬币的直径为1个单位长度,若将硬币沿数轴正方向滚动一周,点
点重合)。假设硬币的直径为1个单位长度,若将硬币沿数轴正方向滚动一周,点 恰好与数轴上点
恰好与数轴上点 重合,则点
重合,则点 对应的实数是
。
对应的实数是
。
17.下列是三种化合物的结构式及分子式,请按其规律,写出后一种化合物的分子式 。

18.在日常生活中如取款、上网等都需要密码,有一种用“因式分解”法产生的密码,方便记忆。原理是:如对于多项式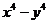 ,因式分解的结果是
,因式分解的结果是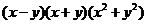 ,若取
,若取 =9,
=9, 时,则各个因式的值是:
时,则各个因式的值是: 。于是就可以把“018162”作为一个六位数的密码。对于多项式
。于是就可以把“018162”作为一个六位数的密码。对于多项式 ,取
,取 时,用上述方法产生的密码是: (写出一个即可)。
时,用上述方法产生的密码是: (写出一个即可)。
19.如下图,将一副直角三角板重叠在一起,使直角顶点重合于点 ,则
,则 。
。

20.计算(本题满分8分)

21.计算(本题满分9分)
某中学图书馆将图书分为自然科学、文学艺术、社会百科、数学四类。在“读书月”活动期间,为了解图书的借阅情况,图书管理员对本月各类图书的借阅量进行了统计。图甲和图乙是图书管理员通过采集数据后,绘制的两幅不完整的频率分布表与频数分布直方图。请你根据图表中提供的信息,解答以下问题:
频率分布表
图书种类
频数
频率
自然科学
400
0.20
文学艺术
1000
0.50
社会百科
500
0.25
数学

图乙 图甲
(1)填充图甲频率分布表中的空格。(2分)
(2)在图乙中,将表示“自然科学”的部分补充完整。(2分)
(3)若该学校打算采购一万册图书,请你估算“数学”类图书应采购多少册较合适?(2分)
(4)根据图表提供的信息。请你提出一条合理化的建议。(2分)
22.证明(本题满分8分)
如图,把平行四边形 翻折,使点
翻折,使点 与点
与点 重合,
重合, 为折痕,连结
为折痕,连结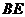 、
、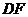 。请你猜一猜四边形
。请你猜一猜四边形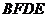 是什么特殊四边形?并证明你的猜想。
是什么特殊四边形?并证明你的猜想。

23.(本题满分l0分)
某商场将每件进价为80元的某种商品原来按每件l00元出售,一天可售出100件,后来经过市场调查,发现这种商品单价每降低l元,其销量可增加l0件。
(1)求商场经营该商品原来一天可获利润多少元?
(2)设后来该商品每件降价 元,商场一天可获利润
元,商场一天可获利润 元。
元。
①若商场经营该商品一天要获利润2160元,则每件商品应降价多少元?
②求出 与
与 之间的函数关系式,并通过画该函数图像的草图,观察其图像的变化趋势,结合题意写出当
之间的函数关系式,并通过画该函数图像的草图,观察其图像的变化趋势,结合题意写出当 取何值时,商场获利润不少于2160元?
取何值时,商场获利润不少于2160元?
24.(本题满分8分)
某校的围墙上端由一段相同的凹曲拱形栅栏组成,如图所示,其拱形图形为抛物线的一部分,栅栏的跨径 间,按相同的间距0.2米用5根立柱加固,拱高
间,按相同的间距0.2米用5根立柱加固,拱高 为0.6米。
为0.6米。

(1)以 为原点,
为原点, 所在的直线为
所在的直线为 轴建立平面直角坐标系,请根据以上的数据,求出抛物线
轴建立平面直角坐标系,请根据以上的数据,求出抛物线 的解析式;
的解析式;
(2)计算一段栅栏所需立柱的总长度。(精确到0.1米)
25.(本题满分8分)
如图,已知 是
是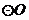 的直径,直线
的直径,直线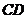 与
与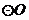 相切于点
相切于点 ,
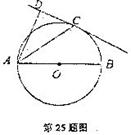
,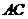 平分
平分 。
。
(1)求证: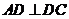 ;
;
(2)若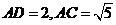 ,求AB的长。
,求AB的长。
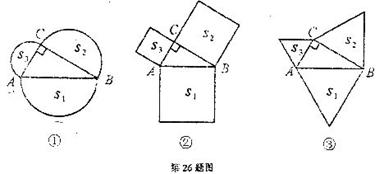
26.(本题满分l2分)
如图①所示,分别以直角三角形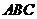 三边为直径向外作三个半圆,其面积分别用、S2、S3表示,则不难证明S1=S2+S3。
三边为直径向外作三个半圆,其面积分别用、S2、S3表示,则不难证明S1=S2+S3。
(1)如图②所示,分别以直角三角形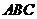 三边为边向外作三个正方形,其面积分别用S1、 S2、S3表示.那么Sl、S2、S3之间有什么关系?(不必证明)
三边为边向外作三个正方形,其面积分别用S1、 S2、S3表示.那么Sl、S2、S3之间有什么关系?(不必证明)
(2)如图③所示,分别以直角三角形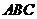 三边为边向外作三个正三角形,其面积分别用Sl、S2、S3表示,请你确定S1、S2、S3之同的关系并加以证明;
三边为边向外作三个正三角形,其面积分别用Sl、S2、S3表示,请你确定S1、S2、S3之同的关系并加以证明;
(3)若分别以直角三角形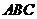 三边为边向外作三个一般三角形,其面积分别用Sl、S2、S3表示,为使Sl、S2、S3之间仍具有与(2)相同的关系,所作三角形应满足什么条件?证明你的结论;
三边为边向外作三个一般三角形,其面积分别用Sl、S2、S3表示,为使Sl、S2、S3之间仍具有与(2)相同的关系,所作三角形应满足什么条件?证明你的结论;
(4)类比(1)、(2)、(3)的结论,请你总结出一个更具一般意义的结论。