2007-2008学年(上)东北师大附中九年级第三次月考
数 学 试 题
一、选择题(每小题3分,共24分)
1.抛物线 的对称轴是
( )
的对称轴是
( )
A.直线x=-3 B.直线x=
2.抛物线y=2x2+3与y轴的交点是 ( )
A.(0,5) B.(0,3) C.(0,2) D.(2,1)
3.一个钢球沿坡角31°的斜坡向上滚动了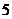 米,此时钢球距地面的高度是(单位:米)( )
米,此时钢球距地面的高度是(单位:米)( )

A.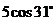 B.
B.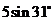 C.
C.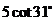 D.
D.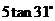
4.若⊙O所在的平面内上有一点P,它到⊙O上的点的最大距离是6,最小距离是2,则这个圆的半径为 ( )
A.2 B.
5.过原点的抛物线是 ( )
A.y=2x2-1 B.y=2x2+
6.如图,是二次函数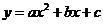 图象的一部分,那么( )
图象的一部分,那么( )

A.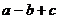 =0 B.
=0 B.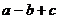 >0
>0
C.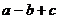 <0 D.
<0 D.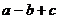 的正、负不能确定
的正、负不能确定
7.圆内接四边形ABCD中,∠A∶∠B∶∠C∶∠D可以是 ( )
A.1∶2∶3∶4 B.1∶3∶2∶
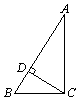
8.如图,在△ABC中,∠ACB=90°,CD⊥AB于D,若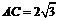 ,
, , 则
, 则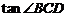 的值为
( )
的值为
( )
A.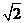 B.
B.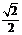 C.
C.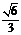 D.
D.
二、填空题(每小题3分,共18分)
9.抛物线 的顶点坐标是
__.
的顶点坐标是
__.
10.如图,一束光线照在坡度为 的斜坡上,被斜坡上的平面镜反射成与地面平行的光线,则这束光线与坡面的夹角
的斜坡上,被斜坡上的平面镜反射成与地面平行的光线,则这束光线与坡面的夹角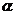 是 °.
是 °.
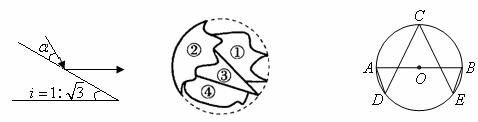
(10题图) (12题图) (13题图)
11.将二次函数y=3(x+2)2-4的图象向右平移3个单位,再向上平移1个单位,所得的图象的函数关系式为_____________________.
12.小明不慎把家里的圆形玻璃打碎了,其中四块碎片如图所示,为配到与原来大小一样的圆形玻璃,小明带到商店去的一块玻璃碎片应该是__________.
13.如图,已知AB是⊙O的直径,点C、D、E都在⊙O上,若∠C=∠D=∠E,则∠A+∠B= º.
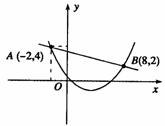
14.已知二次函数y1=ax2+bx+c(a≠0)与一次函数y2=kx+m (k≠0)的图象相交于点A(-2,4),B(8,2),如图,则能使
(k≠0)的图象相交于点A(-2,4),B(8,2),如图,则能使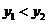 成立的x的取值范围是______ __.
成立的x的取值范围是______ __.
 (14题图)
(14题图)
三、解答题(每小题5分,共20分)
15. tan 45°- sin 60°-2sin2 45°.
sin 60°-2sin2 45°.
16.解方程: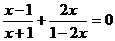 .
.
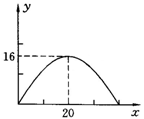
17.如图,有一个抛物线型拱桥,其最大高度为
18.某高速公路是目前我国高速公路隧道和桥梁最多的路段.如图,是一个单心圆曲隧道的截面,若路面AB宽为
四、解答题(每小题6分,共24分)
19.已知二次函数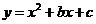 的图象经过A(0,1),B(2,-1)两点.
的图象经过A(0,1),B(2,-1)两点.
(1)求b和c的值;
(2)试判断点P(-1,2)是否在此抛物线上?
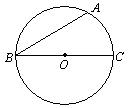
20.已知:在⊙O中, BC是直径,点C和点D是⊙O上的点,且∠ABC=30º,∠DBC=45º,请补全图形,并求出∠AOD的度数.
21.某种商品每件的进价为30元,在某段时间内若以每件x元出售,可卖出(100-x)件,应如何定价才能使利润最大?
22.如图,已知△ABC内接于⊙O,点D在OC的延长线上, ,∠D=30º.
,∠D=30º.
(1)求证:AD是⊙O的切线;
(2)若AC=6,求AD的长.

五、解答题(每小题7分,共14分)
23.抛物线y=2(x-2)2-6的顶点为C,已知y=-kx+3的图象经过点C,求这个一次函数图象与两坐标轴所围成的三角形面积是多少?
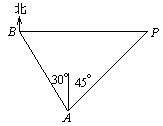
24.一海上巡逻艇在A处巡逻,突然接到上级命令,在北偏西30°方向且距离A处20海里的B港口,有一艘走私艇沿着正东方向以每小时50海里的速度驶向公海,务必进行拦截.巡逻艇马上沿北偏东45°的方向快速追击,恰好在临近公海的P处将走私快艇拦截住.如图所示,试求巡逻艇的速度(结果取整数,参考数据:
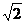 =1.414,
=1.414, =1.732,
=1.732,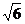 =2.499).
=2.499).

六、解答题(每小题10分,共20分)
25.已知抛物线y=-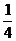 x2-x+1与x轴相交于A、B两点(点A在点B的左侧),与y轴交于C点,它的顶点是点D.
x2-x+1与x轴相交于A、B两点(点A在点B的左侧),与y轴交于C点,它的顶点是点D.
(1)求A、B、C、D各点的坐标;
(2)求△ABC的面积;
(3)求四边形ABCD的面积.
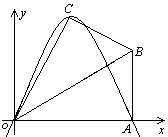
26.已知,在Rt△OAB中,∠OAB=90º,∠BOA=30º,AB=2.若以O为坐标原点,OA所在直线为 轴,建立如图所示的平面直角坐标系,点B在第一象限内.将Rt△OAB沿OB折叠后,点A落在第一象限内的点C处.
轴,建立如图所示的平面直角坐标系,点B在第一象限内.将Rt△OAB沿OB折叠后,点A落在第一象限内的点C处.
(1)求点C的坐标;
(2)若抛物线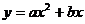 (
(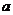 ≠0)经过C、A两点,求此抛物线的解析式;
≠0)经过C、A两点,求此抛物线的解析式;
(3)若抛物线的对称轴与OB交于点D,点P为线段DB上一点,过P作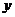 轴的平行线,交抛物线于点M.问:是否存在这样的点P,使得四边形CDPM为等腰梯形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
轴的平行线,交抛物线于点M.问:是否存在这样的点P,使得四边形CDPM为等腰梯形?若存在,请求出此时点P的坐标;若不存在,请说明理由.