2007-2008学年度高密市九年级第一学期期中考试数学试题
(时间90分钟 满分120分)
一、选择题(共10个小题,每小题3分,共30分)
1.要使式子 有意义,字母
有意义,字母 的取值范围必须满足( )
的取值范围必须满足( )
(A) (B)
(B) (C)
(C) (D)
(D)
2.方程 的解是( )
的解是( )
(A) (B)
(B) (C)
(C) (D)
(D)
3.若如图所示的两个四边形相似,则∠α的度数是( )

(A)87° (B)60° (C)75° (D)120°
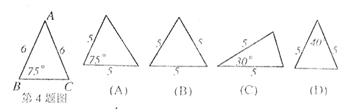
4.下列四个三角形中,与三角形ABC相似的是( )
5.如果2是一元二次方程 的一个根,那么常数
的一个根,那么常数 是( )
是( )
(A)2 (B)-2 (C)4 (D)-4
6.下列方程中有实数根的是( )
(A)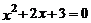 (B)
(B) (C)
(C)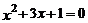 (D)
(D)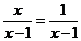
7.下列计算错误的是( )
(A)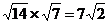 (B)
(B)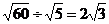
(C)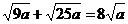 (D)
(D)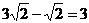
8.下列命题中,真命题的个数是( )
①两个相似多边形的面积之比等于相似比的平方;
②两个相似三角形的对应高之比等于他们的相似比;
③在△ABC和△DEF中,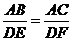 ,∠A=∠D,那么△ABC∽△DEF;
,∠A=∠D,那么△ABC∽△DEF;
④已知△ABC及位似中心O,能够作一个且只能作一个三角形,使位似比为0.5
(A)1个 (B)2个 (C)3个 (D)4个
9.如图,在正方形ABCD中,E是BC的中点,F是CD上一点,且CF= CD,下列结论:①∠BAE=30°,②△ABE∽△AEF,③AE⊥EF,④△ADF∽△ECF.其中正确结论的个数为( )
CD,下列结论:①∠BAE=30°,②△ABE∽△AEF,③AE⊥EF,④△ADF∽△ECF.其中正确结论的个数为( )
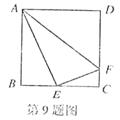
(A)1 (D)2 (C)3 (D)4
10.设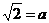 ,
,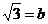 ,用含a,b的式子表示
,用含a,b的式子表示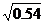 ,则下列表示正确的是( )
,则下列表示正确的是( )
(A)0.3ab (B)3ab (C)0.1ab (D)
二、填空题(共8个小题,每个小题3分,共24分)
11.当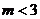 时,
时, =_________________.
=_________________.
12.一元二次方程 ,请你在横线上填一个整数,使该方程有整数解,且能用因式分解法解.
,请你在横线上填一个整数,使该方程有整数解,且能用因式分解法解.
已知 ,
, 是方程
是方程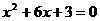 的两实数根,则
的两实数根,则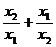 的值为_________.
的值为_________.
14.若梯形的中位线被梯形的两对角线分成三条相等的线段,则此梯形的下底与上底之比为____________.
15.现有一个测试距离为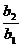 =_______________.
=_______________.

16.如图,在△ABC中,D,E分别是AB和AC的中点,F是BC延长线上的一点,DF平分CE于点G,CF=1,则BC=__________,△ADE与△ABC的 之比为__________,△CFG与△BFD的面积之比为__________.
17.赵亮同学想利用影长测量学校旗杆的高度,他在某一时刻立
18.观察下列各式: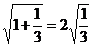 ,
,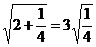 ,
,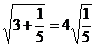 ……请你将发现的规律用含自然数n(n≥1)的等式表示出来______________________.
……请你将发现的规律用含自然数n(n≥1)的等式表示出来______________________.
三、解答题(共8个小题,满分66分)
19.(本题满分6分)计算: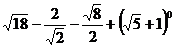
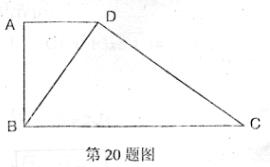
20.(本题满分7分)如图,在梯形ABCD中,AD∥BC,∠BAD=90°,对角线BD上CD.
求证:(1)△ABD∽△DCB;
(2)BD2=AD?BC.
21.(木题满分8分)据报道,我省农作物秸秆的资源巨大,但合理利用量十分有限,2006年的利用率只有30%,大部分秸秆被直接焚烧了。假定我省每年产出的农作物秸秆总量不变,且合理利用量的增长率相同,要使2008年的利用率提高到60%,求每年的增长率.(取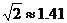 )
)
 .
.
学生甲:老师,这个方程先去括号,在合并同类项,行吗?
老师:这样原方程可整理为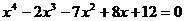 ,次数变成了4次,用现有的知识无法解答.同学们再观察,看看这个方程有什么特点?
,次数变成了4次,用现有的知识无法解答.同学们再观察,看看这个方程有什么特点?
学生乙:老师,我发现方程中 是整体出现的,最好不要去括号!
是整体出现的,最好不要去括号!
教师:很好,我国我们把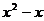 看成一个整体,用
看成一个整体,用 表示,即
表示,即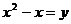 ,那么原方程就变成了
,那么原方程就变成了 .
.
全体学生:(同学们都特别高兴)噢,这不是我们最熟悉的一元二次方程吗?
老师:大家真会观察和思考,太棒了!显然一元二次方程 的根是
的根是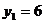 ,
,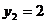 ,那么就有
,那么就有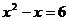 或
或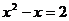 .
.
学生丙:对啦,再解这两个方程,可得原方程的根是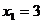 ,
,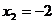 ,
,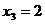 ,
,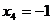 .嗬,有这么多解啊!
.嗬,有这么多解啊!
老师:同学们,通常我们把这种方法叫做换元法.在这里,使用它最大的妙处在于降低方程的次数,这是一种重要的转化方法.
全体学生:OK,换元法真神奇!
现在,请你用换元法解下列分式方程:
 .
.
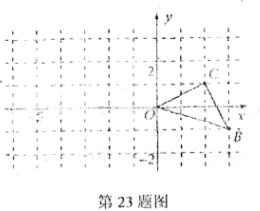
23.(本题满分9分)如图,已知O是坐标原点,B、C两点的坐标分别为(3,-1)、(2,1) .
(1)以O点为位似中心在 轴的左侧将△OBC放大到两倍(即新图与原图的相似比为2),画出图形.
轴的左侧将△OBC放大到两倍(即新图与原图的相似比为2),画出图形.
(2)分别写出B、C 两点的对应点B′、C′的坐标;
(3)如果△OBC内部一点M的坐标为( ,
, ),写出M的对应点M′的坐标.
),写出M的对应点M′的坐标.
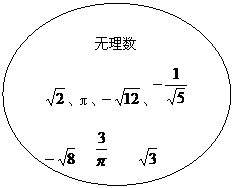
24.(本题满分7分)在下面的两个集合中各有一些实数,请你分别从中选出2个有理数和2个无理数,再用“+、-、×、÷”中的3种符合将选出的4个数进行3次运算,使得运算的结果是一个正整数.




25.(本题满分9分)若0是关于 的方程
的方程 的解,求实数m的值,并讨论此方程的解的情况.
的解,求实数m的值,并讨论此方程的解的情况.
26.(本分满分12分)如图,在△ABC中,AB=AC=1,点D,E在直线BC上运动.设BD= ,CE=
,CE=
(1)如果∠BAC=30°,∠DAE=105°,试确定 与
与 之间的函数关系式;
之间的函数关系式;
(2)如果∠BAC=α,∠DAE=β,当α,β满足怎样的关系时,(1)中 与
与 之间的函数关系式还成立?试说明理由.
之间的函数关系式还成立?试说明理由.
