2006-2007学年度东营市第二学期期末质量调研
初三数学试卷
一.选择题:本题共12小题,每小题4分,满分48分。下面各题给出的四个选项中,只有一项是正确的,请将正确选项的代号填在题后的括号内。
1.三角形在正方形网格纸中的位置如图所示,则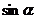 的值是
的值是

A. B.
B.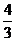 C.
C.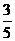 D.
D.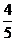
2.计算tan60°+2sin45°-2cos30°的结果是
A.2 B.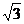 C.
C. 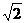 D.1
D.1
3.如下图,是一水库大坝横断面的一部分,坝高h=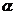 ,则
,则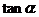 的值为
的值为

A.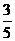 B.
B.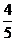 C.
C.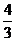 D.
D.
4.小明从二次函数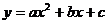 图像中,观察得出了下面的五条信息:
图像中,观察得出了下面的五条信息:

① ;②
;② ;③函数的最小值为-3;④当
;③函数的最小值为-3;④当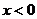 时,
时,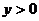 ;⑤当
;⑤当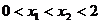 时,
时, 。你认为其中正确的有 个。
。你认为其中正确的有 个。
A.2 B.
5.已知 的图像是抛物线,若抛物线不动,把
的图像是抛物线,若抛物线不动,把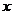 轴、
轴、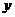 轴分别向上、向右平移2个单位,那么在新坐标系下抛物线的解析式是
轴分别向上、向右平移2个单位,那么在新坐标系下抛物线的解析式是
A.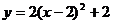 B.
B.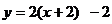
C.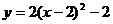 D.
D.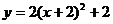
6.如下图,是抛物线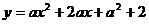 的―部分图像,那么抛物线与
的―部分图像,那么抛物线与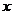 轴另―交点坐标为
轴另―交点坐标为

A. B.
B. C.
C.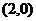 D.
D.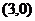
7.老师出示了小黑板上的题后(如下图),小华说:过点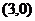 ;小彬说:过点
;小彬说:过点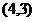 ;小明说:
;小明说: ;小颖说:抛物线被
;小颖说:抛物线被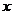 轴截得的线段长为2。你认为四人的说法中,正确的有
轴截得的线段长为2。你认为四人的说法中,正确的有

A.1个 B.2个 C.3个 D.4个
8.如下图,⊙O的直径CD过弦EF的中点G,∠EOD=40°,则∠DCF等于
A.80° B.50° C.40° D.20°

9.已知⊙O的半径为3cm,点P是直线 上―点,OP长为5cm,则直线
上―点,OP长为5cm,则直线 与⊙O的位置关系为
与⊙O的位置关系为
A.相交 B.相切
C.相离 D.相交、相切、相离都有可能
10.如下图,圆锥的母线长是 ,底面半径是
,底面半径是 ,A是底面圆周上一点,从点A出发绕侧面一周,再回到点A的最短的路线长是
,A是底面圆周上一点,从点A出发绕侧面一周,再回到点A的最短的路线长是

A.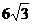 B.
B.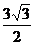 C.
C.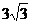 D.
D.
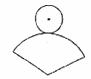
11.如下图,在纸上剪下一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型.若圆的半径为 ,扇形的半径为
,扇形的半径为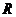 ,扇形的圆心角等于120°,则
,扇形的圆心角等于120°,则 与
与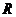 之间的关系是
之间的关系是
A.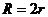 B.
B. C.
C. D.
D.
12.如下图,半圆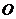 的直径AB=4,与半圆
的直径AB=4,与半圆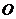 内切的动圆
内切的动圆 ,与AB切于点M,设圆
,与AB切于点M,设圆 的半径为
的半径为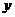 ,AM=
,AM=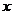 ,则
,则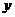 关于
关于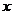 的函数关系式是
的函数关系式是
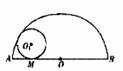
A. B.
B.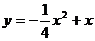 C.
C. D.
D.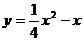
二、填空题:本大题共5小题,共20分,只要求填写最后结果,每小题填对得4分。
13.在位于O处某海防哨所的北偏东60°相距6海里的A处,有一艘快艇正向正南方向航行,经过一段时间快艇到达哨所东南方向的B处,则A、B间的距离是
海里。(精确到0.1海里,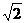 ≈1.414,
≈1.414, 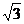 ≈1.732)
≈1.732)
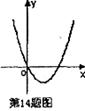
14.如图是二次函数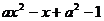 的图像,则
的图像,则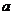 的值是 。
的值是 。
15.已知等腰△ABC的外接圆⊙O的半径为5,如果等腰△ABC的底边BC的长为6,则底角的正切值为 。
16.数字解密:第―个数是3=2+1,第二个数是5=3+2,第三个数是9=5+4,第四个数是l7=9+8,……,观察并猜想第六个数是 。
17.2006年世界杯足球赛在德国举行,本次比赛共32支球队平均分成8个小组首先进行小组赛,每小组内举行单循环比赛(每个球队都与本小组的其它队比赛一场),选出两个球队进入16强.本次足球赛的小组赛共进行 场比赛。
三、解答题:本大题共8小题。共82分.解答要写出必要的文字说明、证明过程或演算步骤。18.(本题满分8分)
如下图所示,某船向正东方向航行,在A处望见某岛C在北偏东60°方向,前进6海里到B点,测得该岛在北偏东30°方向。已知该岛周围6海里内有暗礁,若该船继续向东航行,有无触礁危险?请说明理由。(参考数据: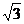 =1.732)
=1.732)

19.(本题满分l4分)
如下图,小山的顶部是一块平地,在这块平地上有一高压输电的铁架,小山的斜坡的坡度 ,斜坡BD的长是50米,在山坡的坡底B处测得铁架顶端A的仰角为45°,在山坡的坡顶D处测得铁架顶端的仰角为60°。
,斜坡BD的长是50米,在山坡的坡底B处测得铁架顶端A的仰角为45°,在山坡的坡顶D处测得铁架顶端的仰角为60°。

(1)求小山的高度;
(2)求铁架的高度。(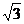 ≈1.73,精确到0.1米)
≈1.73,精确到0.1米)
20.(本题满分l2分)
某商场购进一种单价为40元的篮球,如果以单价50元出售,那么每月可售出500个,根据销售经验,售价每提高1元,销售量相应减少l0个;
(1)假设销售单价提高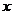 元,那么销售每个篮球所获得的利润是 元;这种篮球每月的销售量是 个;(用含
元,那么销售每个篮球所获得的利润是 元;这种篮球每月的销售量是 个;(用含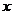 的代数式表示)
的代数式表示)
(2)8000元是否为每月销售这种篮球的最大利润?如果是,请说明理由;如果不是,请求出最大利润,此时篮球的售价应定为多少元?
21.(本题满分8分)
如下图所示,有一座抛物线形拱桥,桥下面在正常水位AB时,宽20m,水位上升3m就达到警戒线CD,这时水面宽度为10m。
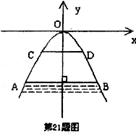
(1)在如上图的坐标系中求抛物线的解析式;
(2)若洪水到来时,水位以每小时0.2m的速度上升,从警戒线开始,再持续多少小时才能到达拱桥顶?
22.(本题满分l2分)
如下图,已知O为原点,点A的坐标为(4,3),⊙A的半径为2,过A作直线 平行于
平行于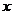 轴,点P在直线
轴,点P在直线 上运动。
上运动。
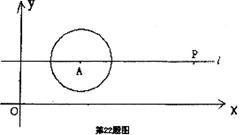
(1)当点P在⊙O上时,请你直接写出它的坐标;
(2)设点P的横坐标为12,试判断直线OP与⊙A的位置关系,并说明理由。
23.(本题满分l0分)
某商场设计了两种促销方案:第一种是顾客在商场消费每满200元就可以从一个装有100个完全相同的球(球上分别标有数字l,2,……,l00)的箱子中随机摸出一个球(摸后放回)。若球上的数字是88,则返购物券500元;若球上的数字是11或77,则返购物券300元;若球上的数字能被5整除,则返购物券5元;若是其它数字,则不返购物券。第二种是顾客在商场消费每满200元直接获得购物券l5元。估计促销期间将有5000人次参加活动。请你通过计算说明商家选择哪种促销方案合算些?
24.(本题满分8分)
甲乙两人在玩转盘游戏时,把转盘A、B分别分成4等份、3等份,并在每一份内标上数字,如下图所示。游戏规定,两个转盘停止转动后,指针所指的两个数字之和为奇数时,甲获胜;为偶数时,乙获胜。
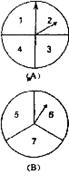
(1)用列表法(或画树状图)求甲获胜的概率;
(2)你认为这个游戏规则对双方公平吗?请简要说明理由。
25.(本小题满分l0分)
如下图在⊙O的内接△ABC中,AB+AC=12,AD⊥AC,垂足为D,且 AD=3,设⊙O的半径为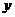 ,AB的长为
,AB的长为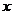 。
。

(1)求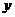 与
与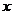 的函数关系式;
的函数关系式;
(2)当AB的长等于多少时,⊙A的面积最大,并求出⊙O的最大面积。