2006-2007学年度第二学期期末考试八年级数学试卷
(时间90分钟 满分120分)
一、选择题(每小题3分,共30分)
1.数据10,10,10,11,12,12,15,15的众数是( )
A.10 B.
2.在下列命题中,正确的是( )
A.一组对边平行的四边形是平行四边形 B.有一个角是直角的四边形是矩形
C.有一组邻边相等的平行四边形是菱形 D.对角线互相垂直平分的四边形是正方形
3.对于反比例函数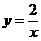 ,下列说法不正确的是( )
,下列说法不正确的是( )
A.点(-2,-1)在它的图象上 B.它的图象在第一、三象限
C.当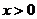 时,
时,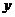 随
随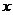 的增大而增大 D.当
的增大而增大 D.当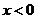 时,
时,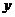 随
随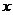 的增大而减小
的增大而减小
4.解分式方程: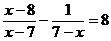 ,可知此方程( )
,可知此方程( )
A.解为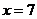 B.解为
B.解为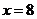 C.解为
C.解为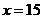 D.无解.
D.无解.
5.函数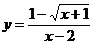 中,自变量
中,自变量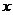 的取值范围是( )
的取值范围是( )
A.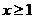 B.
B.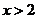 C.
C.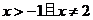 D.
D.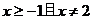
6.下列计算正确的是( )
A.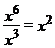 B.
B.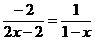 C.
C.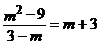 D.
D.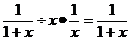
7.如图,已知∠1=∠2,AC=AD;增加下列条件:①AB=AE;②BC=ED;③∠C=∠D;④∠B=∠E.其中能使△ABC≌△AED的条件有( )
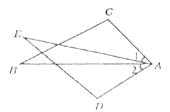
A.4个 B.3个 C.2个 D.1个
8.如图,已知线段a,h作等腰△ABC,使AB=AC,且BC=a,BC边上的高AD=h.张红的作法是:(1)作线段BC=a;(2)作线段BC的垂直平分线MN,MN与BC相交于点D;(3)在直线MN上截取线段h;(4)连结AB,AC,△ABC为所求的等腰三角形.上述作法的四个步骤中,有错误的一步你认为是
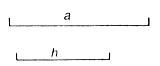
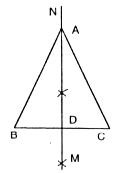
A.(1) B.(2) C.(3) D.(4)
9.某学校举行理科(含数学、物理、化学、生物四科)综合能力比赛,四科的满分都为100分.甲、乙、丙三人四科的测试成绩如下表:
学科
数学
物理
化学
生物
甲
95
85
85
60
乙
80
80
90
80
丙
70
90
80
95
综合成绩按照数学、物理、化学、生物四科测试成绩的1.2:1:1:0.8的比例计分,则综合成绩的第一名是( )
A.甲 B.乙 C.丙 D.不确定
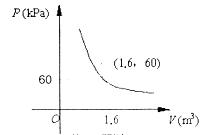
10.某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.当气球内的气压大于120 kPa时,气球将爆炸.为了安全起见,气球的体积应( )
A.不小于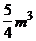 B.小于
B.小于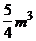 C.不小于
C.不小于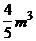 D.小于
D.小于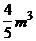
二、填空题(每小题3分,共24分)
11.计算: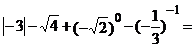 ___________.
___________.
12.我们知道,1纳米=10
13.如图,已知函数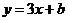 和
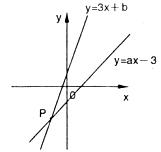
和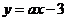 的图像交于点P(-2,-5),则根据图像可得不等式
的图像交于点P(-2,-5),则根据图像可得不等式 的解集是_________________
的解集是_________________
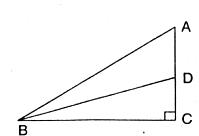
14.如图,在Rt△ABC中,∠C=90'°,BD是直角三角形的角平分线,交AC于点D,AD=
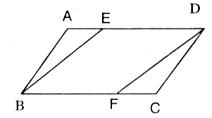
15.如图,在平行四边形ABCD中,E、F分别为AD、BC边上一点,若再增加一个条件_______,就可推得BE=DF.
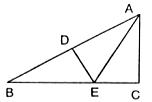
16.如图,DE是△ABC的边AB的垂直平分线,分别交AB、BC于D、E,AE平分∠BAC,若∠B=30°,则∠C的度数是_________________.
17.人民商场对上周女装的销售情况进行了统计,如下表所示:
颜色
黄色
绿色
白色
紫色
红色
数量(件)
100
180
220
80
550
经理决定本周进女装时多进一些红色的,可用来解释这一现象的统计知识是___________(从平均数,中位数,众数,方差中选一个).
18.在四边形ABCD中,对角线AC、BD交于点O,从(1)AB=CD;(2)AB∥CD;(3)OA=OC;(4)OB=OD;(5)AC⊥BD;(6)AC平分∠BAD这六个条件中,选取三个推出四边形ABCD是菱形.如(1)、(2)、(5)
 ABCD是菱形,再写出符合要求的两个:________________
ABCD是菱形,再写出符合要求的两个:________________
 ABCD是菱形;____________________
ABCD是菱形;____________________
 ABCD是菱形.
ABCD是菱形.
三、解答题(共8个小题,共66分)
19.(本题满分6分)课堂上,李老师给大家出了这样一道试题:当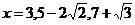 时,求代数式
时,求代数式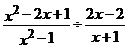 的值.小明一看,“太复杂了,怎么算呢?”你能帮小明解决这个问题吗?请你写出具体过程.
的值.小明一看,“太复杂了,怎么算呢?”你能帮小明解决这个问题吗?请你写出具体过程.
20.(本题满分7分)如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,A,C,D三点在同一直线上,连结BD,AE,并延长AE交BD于F.
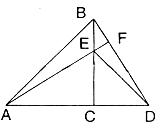
(1)求证:△ACE≌△BCD.
(2)直线AE与BD互相垂直吗?请证明你的结论.
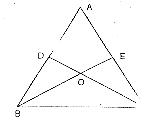
21.(本题满分8分)如图,D、E分别为△ABC的边AB、AC上的点,BE与CD相交,现有四个条件:①AB=AC;②,OB=OC;③∠ABE=∠ACD;④BE=CD.
 c
c
(1)请你选出两个条件作为假设,余下的两个作为结论,写出一个正确的命题的条件是______和________,命题的结论是________和________(均填序号).
(2)证明你写出的命题.
已知:
求证:
证明:
22.(本题满分8分)
小明在超市帮妈妈买回一袋纸杯,他把纸杯整齐地叠放在桌面上,请你根据图中的信息,解答下列问题.
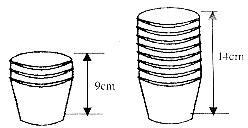
(1)求整齐叠放在桌面上纸杯的高度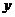 (cm)与纸杯数
(cm)与纸杯数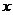 (个)之间的一次函数关系式(不要求写出自变量的取值范围).
(个)之间的一次函数关系式(不要求写出自变量的取值范围).
(2)若小明把100个纸杯整齐叠放在一起时,求它的高度.
23.(本题满分8分)
某学校举行演讲比赛,选出了10名同学担任评委,并事先拟定从如下4个方案中选择合理的方案来确定每个演讲者的最后得分(满分为10分):
方案1 所有评委所给分的平均数.
方案2 在所有评委所给分中,去掉一个最高分和一个最低分,然后再计算其余给分的平均数.
方案3 所有评委所给分的中位数.
方案4 所有评委所给分的众数.
为了探究上述方案的合理性,先对某个同学的演讲成绩进行了统计实验.下面是这个同学的得分统计图:

分别按上述4个方案计算这个同学演讲的最后得分;
(2)根据(1)中的结果,请用统计的知识说明哪些方案不适合作为这个同学演讲的最后得分.
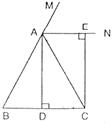
24.(本题满分10分)已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,
(1)求证:四边形ADCE为矩形.
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.
25.(本题满分10分)张老师承公交车上班,从家到学校有A、B两条路线可选择.他作了一番实验,第一周:星期一,星期三,星期五选A路线,星期二,星期四选B路线,每天两趟,第二周交换.记录所用时间如下表:(单位:分)
实验序号
1
2
3
4
5
6
7
8
9
10
A路线所花时间
31
51
36
36
58
43
42
32
52
39
B路线所花时间
46
50
41
43
47
48
49
48
43
45
根据两条路线所花的时间绘制的折线统计图如图所示

(1)观察图,请说明选择哪条路线乘车用时较少,选择哪条路线乘车用时的波动较大;
(2)计算选择A、B两条路线乘车所用时间的平均数和方差并作出合理的解释;
(3)如果上班路上的可用时间只有40分,乘车应选择哪条路线?
(4)如果路上可用时间为50分,乘车应选择哪条路线?
26.(本题满分9分)如图,已知直线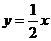 与双曲线
与双曲线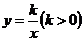 交于A、B两点,且点A的横坐标为4.
交于A、B两点,且点A的横坐标为4.
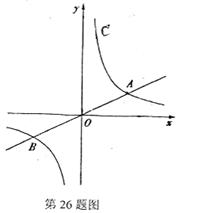
(1)求k的值;
(2)若双曲线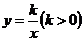 上一点C的纵坐标为8,求△AOC的面积.
上一点C的纵坐标为8,求△AOC的面积.