2006-2007学年度淄博市淄川区第二学期期末考试
初三数学试卷
一、精心选一选(本题共l2小题.在每小题所给出的四个选项中,只有一个是正确的,请选出你认为唯一正确的答案,每小题3分,计36分).
1.在下列图形中,沿着虚线将矩形剪成两部分,那么由这两部分既能拼成三角形,又能拼成平行四边形和梯形的是 ( )

(A) (B) (C) (D)
2.若a、b为实数,满足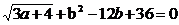 ,则ab的值为 ( )
,则ab的值为 ( )
(A)4 (B)-4 (C)-8 (D)8
3.将l00个个体的样本变成组号为①~⑧个组,如下表:
组号
l
2
3
4
5
6
7
8
频数
14
12
13
■■
13
12
10
那么第五组的频率是 ( )
(A)14 (B)15 (C)0.14 (D)0.15
4.下列方程没有实数根的是 ( )
(A) 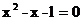 (B)
(B)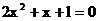
(C) 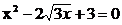 (D)x2―6x+5=0
(D)x2―6x+5=0
5.在△ABC和 △A′B′ C′① AB=A′B′ ②BC=B′C′③AC=A′C′④∠A=∠A′⑤∠B=∠B′⑥∠C=∠C′,则下列条件中,不能保证△ABC≌△A′B′ C′的是( )
(A)①②③ (B)①②⑤ (C)②④⑤ (D)①③⑤
6.在做“抛掷两枚硬币实验”时,有部分同学没有硬币,因而需要选用别的实物来代替进行实验,在以下所选用的替代物中,你认为较合适的是( )
(A)两张扑克牌,一张是红桃,另一张是黑桃
(B)两个乒乓球,一个是黄色,另一个是白色
(C)两个相同的矿泉水瓶盖
(D)四张扑克牌,两张红桃,另两张是黑桃
7.如图,以正方形ABCD的一边向外作等边△ABE,BD与EC交于F,则∠AFD等于 ( )
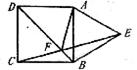
(A)60° (B)50° (C)45° (D)40°
8.若关于x的一元二次方程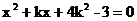 的两个实数根分别是xl,x2,且满足
的两个实数根分别是xl,x2,且满足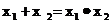 .则k的值是 ( )
.则k的值是 ( )
(A)-1或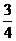 (B)-1 (C)
(B)-1 (C) 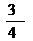 (D)不存在
(D)不存在
9.反比例函数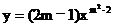 ,当x>0时,y随x的增大而增大,则m的值是 ( )
,当x>0时,y随x的增大而增大,则m的值是 ( )
(A)±1 (B)-1 (C)1 (D)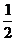
10.梯形ABCD中,E为腰BC的中点,若AB=8,CD=2,AE把梯形分为△ABE和四边形ADCE,它们的周长相差4,则梯形腰AD长为( )
(A)12 (B)10 (C)2或10 (D)2或12
11.已知正比例函数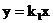 (k1≠0)与反比例函数
(k1≠0)与反比例函数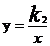 (K2≠0)的图象有一个交点的坐标为
(K2≠0)的图象有一个交点的坐标为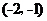 ,则它们的另一个交点的坐标是 ( )
,则它们的另一个交点的坐标是 ( )
(A) (2,1) (B) (-2,-l) (C) (-2,1) (D) (2,l)
12.如图在矩形ABCD中,AB=3,AD=4,P是AD边上的一个动点,PE⊥AC于E,PF⊥BD于F, 则PE+PF的值 ( )
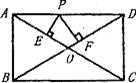
(A) 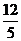 (B) 2 (C)
(B) 2 (C) 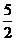 (D)
(D) 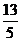
二、细心填一填(本题共8小题,满分32分,只要求填写最后结果,每小题填对得4分)。
13.如图,△ABC是直角三角形,BC是斜边,将△ABP绕点A按逆时针方向旋转后,能与△ACP′重合,若AP=4,则PP′的长是 。

14.在对某次实验次数整理过程中,某个事件出现的频率随实验次数变化折线图如图所示,这个图中折线变化的特点是: ,该事件发生的概率是 。

15、已知关于x的方程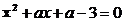 有一个正数根和一个负数根,则a的取值范围是 。
有一个正数根和一个负数根,则a的取值范围是 。
16.已知点A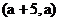 和点B
和点B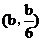 是同一个反比例函数图象上的两点,则这个反比例函数的关系式是 。
是同一个反比例函数图象上的两点,则这个反比例函数的关系式是 。
17.如图,□ABCD中,P是CD上的一点, 且AP和BP分别平分∠DAB和∠CBA,PQ∥AD, 若AD=
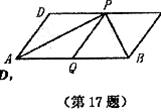
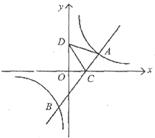
18.如图是一次函数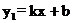 和反比例函数
和反比例函数 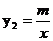 的图象,观察图象写出y1>y2时,x的取值范围是
。
的图象,观察图象写出y1>y2时,x的取值范围是
。

19.现有A、B两枚均匀的小立方体(立方体的每个面分别标有l,2,3,4,5,6).用小明A立方体朝上的数字为x,小亮掷B立方体朝上的数字为y来确定点P(x,y),那么他们各掷一次所确定的点P落在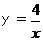 上的概率是 。
上的概率是 。
20.已知菱形ABCD的边长为6,∠A=60°,如果点P是菱形内的一点,且PB=PD=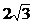 ,那么AP的长是 。
,那么AP的长是 。
三、耐心做一做,相信你能写出正确的解答过程(共52分,注意审题要细心,书写要规范和解答要完整).
21.(本题满分l2分)
(1)解方程: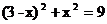
(2)某种药品两次降价后,每盒售价从6.4元降到4.9元.平均每次降价百分之几?
22.(本题满分9分)
如图,有两组扑克牌,每组中备有3张牌,它们的牌面数字分别是1,2,3.从每组中各随机摸出一张牌.
(1)一共有多少种不同的结果?(用树状图或列表格加以说明)
(2)两张牌牌面数字之和为几的概率最大?最大的概率是多少?
23.(本题满分l0分)
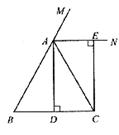
已知:如图在△ABC中,AB=AC,AD⊥BC,垂足为D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为E。
(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.
24.(本题满分l0分)
如图,已知点A(4,m),B(一1,n)在反比例函数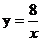 的图象上,直线AB与x轴交于点C.如果点D在y轴上,且DA=DC,请解决以下问题:
的图象上,直线AB与x轴交于点C.如果点D在y轴上,且DA=DC,请解决以下问题:
(1) 填空:m= ,n= .
(2) 求直线AB的解析式;
(3)点D的坐标.
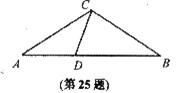
25.(本题满分ll分)
已知:如图,在△ABC中,D是AB边上的点,∠A=36°,AC=BC,AC2=AB•AD.
(1)试说明:△ADC和△BDC都是等腰三角形;
(2)若AB=1,求AC的值: ’
(3)试构造一个等腰梯形,该梯形连同它的两条对角线,得到了8个三角形,要求构造出的图形中有尽可能多的等腰三角形.(标明各角的度数)