2007年广东省初中毕业生学业考试
数 学
(本试卷考试时间为100分钟,满分120分)
一.选择题(本大题共5小题,每小题3分,共15分)在每小题给出的四个选项中,只有一个是正确的,请将所选选项的字母写在题目后面的括号内。
1.2006年广东省国税系统完成税收收入人民币3.450 65×1011元,连续12年居全国首位,也就是收入了( )。
A、345.065亿元 B、3 450.65亿元 C、34 506.5亿元 D、345 065亿元
2.在三个数0.5、 、
、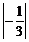 中,最大的数是(
)。
中,最大的数是(
)。
A、0.5 B、 C、
C、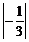 D、不能确定
D、不能确定
3.下列各式中,能用平方差公式分解因式的是( )。
A、x2+4y2 B、x2-2y+1 C、-x2+4y2 D、-x2-4y2
4.袋中有同样大小的4个小球,其中3个红色,1个白色。从袋中任意地同时摸出两个球,这两个球颜色相同的概率是( )。
A、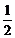 B、
B、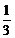 C、
C、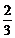 D、
D、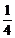
5.到三角形三条边的距离都相等的点是这个三角形的( )。
A、三条中线的交点 B、三条高的交点
C、三条边的垂直平分线的交点 D、三条角平分线的交点
二.填空题(本大题共5小题,每小题4分,共20分)
 请把下列各题的正确答案填写在横线上。
请把下列各题的正确答案填写在横线上。
6.由2点15分到2点30分,时钟的分针转过的角度是__________。
7.如图,在不等边△ABC中,DE∥BC,∠ADE=60°,图中等于60°的角还有__________________。
 8.池塘中放养了鲤鱼8000条,鲢鱼若干。在几次随机捕捞中,共抓到鲤鱼320条,鲢鱼400条。估计池塘中原来放养了鲢鱼__________条。
8.池塘中放养了鲤鱼8000条,鲢鱼若干。在几次随机捕捞中,共抓到鲤鱼320条,鲢鱼400条。估计池塘中原来放养了鲢鱼__________条。
9.已知a、b互为相反数,并且3a-2b=5,则a2+b2=___________。
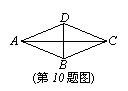
10.如图,菱形ABCD的对角线AC=24,BD=10,则菱形的周长L=________。
三.解答题(本大题共5小题,每小题6分,共30分)
 11.计算:
11.计算: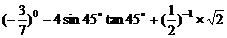
12.已知不等式x+8>4x+m(m是常数)的解集是x<3,求m。
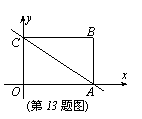
13.如图,在直角坐标系中,已知矩形OABC的两个顶点坐标A(3,0),B(3,2),对角线AC所在直线为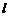 ,求直线
,求直线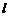 对应的函数解析式。
对应的函数解析式。
14.如图,Rt△ABC的斜边AB=5,cosA=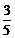 。
。
(1)用尺规作图作线段AC的垂直平分线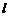 (保留作图痕迹,不要求写作法、证明);
(保留作图痕迹,不要求写作法、证明);
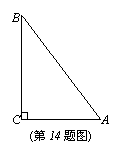 (2)若直线
(2)若直线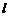 与AB、AC分别相交于D、E两点,求DE的长。
与AB、AC分别相交于D、E两点,求DE的长。
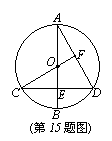 15.如图,已知⊙O的直径AB垂直弦CD于点E,连结CO并延长交AD于点F,若CF⊥AD,AB=2,求CD的长。
15.如图,已知⊙O的直径AB垂直弦CD于点E,连结CO并延长交AD于点F,若CF⊥AD,AB=2,求CD的长。
四.解答题(本大题共4小题,每小题7分,共28分)
16.某文具厂加工一种学生画图工具2500套,在加工了1000套后,采用了新技术,使每天的工作效率是原来的1.5倍,结果提前5天完成任务,求该文具厂原来每天加工多少套这种学生画图工具。
17.两块含30°角的相同直角三角板,按如图位置摆放,使得两条相等的直角边AC、C1A1共线。
(1)问图中有多少对相似三角形,多少对全等三角形?并将他们写出来;
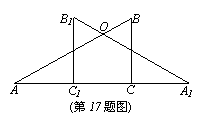 (2)选出其中一对全等三角形进行证明。(△ABC≌△A1B1C1除外)
(2)选出其中一对全等三角形进行证明。(△ABC≌△A1B1C1除外)
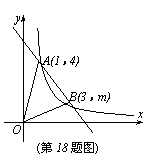 18.如图,在直角坐标系xOy中,一次函数y=k1x+b的图象与反比例函数
18.如图,在直角坐标系xOy中,一次函数y=k1x+b的图象与反比例函数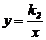 的图象交于A(1,4)、B(3,m)两点。
的图象交于A(1,4)、B(3,m)两点。
(1)求一次函数的解析式;
(2)求△AOB的面积。
19.一粒木质中国象棋子“兵”,它的正面雕刻一个“兵”字,它的反面是平的。将它从一定高度下掷,落地反弹后可能是“兵”字面朝上,也可能是“兵”字面朝下。由于棋子的两面不均匀,为了估计“兵”字面朝上的概率,某实验小组做了棋子下掷实验,实验数据如下表:
实验次数
20
40
60
80
100
120
140
160
“兵”字面朝上频数
14
38
47
52
66
78
88
相应频率
0.7
0.45
0.63
0.59
0.52
0.56
0.55
(1)请将数据表补充完整;
(2)画出“兵”字面朝上的频率分布折线图;
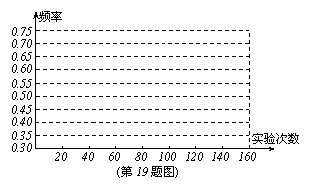

(3)如图实验继续进行下去,根据上表的数据,这个实验的频率将稳定在它的概率附近,请你估计这个概率是多少?
五.解答题(本大题共3小题,每小题9分,共27分)
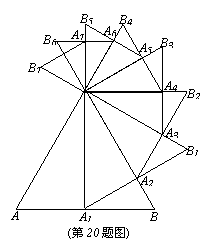
20.已知等边△OAB的边长为a,以AB边上的高OA1为边,按逆时针方向作等边△OA1B1,A1B1与OB相交于点A2。
(1)求线段OA2的长;
(2)若再以OA2为边按逆时针方向作等边△OA2B2,A2B2与OB1相交于点A3,按此作法进行下去,得到△OA3B3,△OA4B4,…,△OAnBn(如图)。求△OA6B6的周长。

21.如图①、②,图①是一个小朋友玩“滚铁环”的游戏,铁环是圆形的,铁环向前滚动时,铁环钩保持与铁环相切。将这个游戏抽象为数学问题,如图②。已知铁环的半径为5个单位(每个单位为5cm),设铁环中心为O,铁环钩与铁环相切点为M,铁环与地面接触点为A,∠MOA=α,且sinα=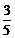 。
。
(1)求点M离地面AC的高度BM(单位:厘米);
(2)设人站立点C与点A的水平距离AC等于11个单位,求铁环钩MF的长度(单位:厘米)。
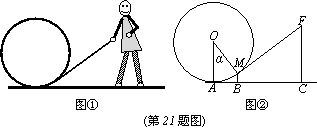

22.如图,正方形ABCD的边长为3a,两动点E、F分别从顶点B、C同时开始以相同速度沿BC、CD运动,与△BCF相应的△EGH在运动过程中始终保持△EGH≌△BCF,对应边EG=BC,B、E、C、G在一直线上。
(1)若BE=a,求DH的长;
(2)当E点在BC边上的什么位置时,△DHE的面积取得最小值?并求该三角形面积的最小值。

