2007年济南市市中区九年级模拟考试
数学试卷
第I卷 (选择题 共48分)
注意事项:
1.数学考试中允许使用不含存储功能的计算器。
2.答第I卷前,考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上。
3.选择题为四选一题目,每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其它答案。不能答在测试卷上。
4.考试结束,监考教师将本试卷和答题卡一并收回。
一、选择题:本大题共12个小题.每小题4分;共48分.在每小题给出的四个选项中,只有一项是符合题目要求的。
1.计算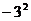 所得结果正确的是 ( )
所得结果正确的是 ( )
A.9 B.-6 C.-9 D.6
2.吸烟有害健康.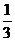 .用科学记数法表示全世界吸烟人数约为 ( )
.用科学记数法表示全世界吸烟人数约为 ( )
A. B.
B.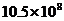 C.
C. D.
D.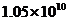
3.甲、乙两袋均有红、黄色球各一个,分别从两袋中任意取出一球,那么所取出的两球是同色球的概率为 ( )
A.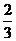 B.
B. C.
C.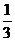 D.
D.
4.已知两圆的半径分别是一元二次方程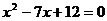 的两个根,若这两个圆的圆心距为5,则这两个圆的位置关系是 ( )
的两个根,若这两个圆的圆心距为5,则这两个圆的位置关系是 ( )
A.相离 B.外切 C.相交 D.内切
5.下面式子从左边到右边的变形中是因式分解的是 ( )
A.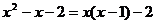 B.
B.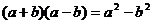
C.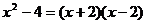 D.
D.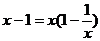
6.在一个四边形ABCD中,依次连结各边中点的四边形是菱形,则对角线AC与BD需要满足条件 ( )
A.垂直 B.相等 C.垂直且相等 D.不再需要条件
7.在平面直角坐标系中,若点P(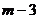 ,
,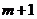 )在第三象限,则
)在第三象限,则 的取值范围为 ( )
的取值范围为 ( )
A.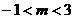 B.
B.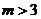 C.
C. D.
D.
8.水果店用1000元购进一批草莓,当天售出获利10%,过几天后又以上次收回资金的90%购进另一批草莓,由于天气变化卖不出去,一天后将这批草莓按第二次购进价的九折(即90%)降价售出。这样,这家水果店在这两次交易中 ( )
A.赢利1元 B.赢亏平衡 C.赢利9元 D.亏本11元
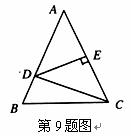
9.在△ABC中,已知AB=AC,DE垂直平分AC,∠A=50°,则∠DCB的度数是 ( )
A.15° B.30° C.50° D.65°
10.命题“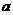 、
、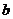 是实数,若
是实数,若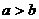 ,则
,则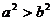 ”若结论保持不变,怎样改变条件,命题才是真命题,以下四种改法:
”若结论保持不变,怎样改变条件,命题才是真命题,以下四种改法:
(1)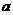 、
、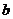 是实数,若
是实数,若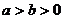 ,则
,则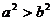 ;(2)
;(2) 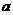 、
、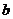 是实数,若
是实数,若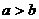 且
且 ,则
,则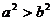 (3)
(3) 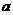 、
、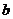 是实数,若
是实数,若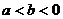 ,则
,则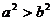 ;(4)
;(4) 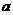 、
、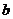 是实数,若
是实数,若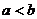 且
且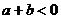 ,则
,则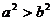 。其中真命题的个数是 ( )
。其中真命题的个数是 ( )
 A.1个 B.3个 C.2个 D.4个
A.1个 B.3个 C.2个 D.4个
11.已知函数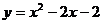 的图像如图所示,根据其中提供的信息,可求得使
的图像如图所示,根据其中提供的信息,可求得使 成立的
成立的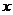 的取值范围是 ( )
的取值范围是 ( )
A. B.
B.
C. D.
D.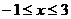
12.如图,已知边长为2的正三角形ABC沿着直线l滚动。设△ABC滚动240°时,C点的位置为 ,△ABC滚动480°时,A点的位置为
,△ABC滚动480°时,A点的位置为 。请你利用三角函数中正切的两角和公式
。请你利用三角函数中正切的两角和公式 ,求出∠CA
,求出∠CA +∠CA
+∠CA 的度数。
的度数。
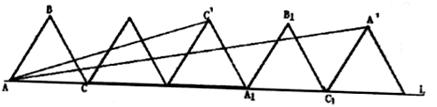
A.30° B.90° C.60° D.45°
第Ⅱ卷 (非选择题 共72分)
注意事项:
1.第Ⅱ卷共6页,用蓝、黑钢笔或圆珠笔直接备在试卷上.
2.答卷前将密封线内的项目填写清楚.
二、填空题:本大题共5个小题,每小题3分,共15分,把答案填在题中横线上。
13.下列各数: 、
、 、
、 、
、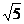 、0.01020304…中是无理数的有______________________。
、0.01020304…中是无理数的有______________________。
14.为了估计池塘里有多少条鱼,从池塘里捕捞了1000条鱼做上标记,然后放回池塘里,经过一段时间,等有标记的鱼完全混合于鱼群中以后,再捕捞200条,若其中有标记的鱼有10条,则估计池塘里有鱼__________________条.
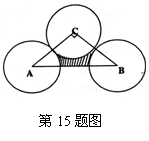
15.如图,在Rt△ABC中,∠C=90°,AC=BC=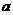 ,分别以A、B、C为圆心,以
,分别以A、B、C为圆心,以 AC为半径画弧,三条弧与边AB所围成的阴影部分面积为__________________.(保留
AC为半径画弧,三条弧与边AB所围成的阴影部分面积为__________________.(保留 )
)

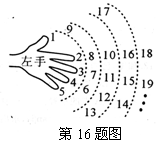

16.在很小的时候,我们就用手指练习过数数.一个小朋友按如图所示的规则练习数数,数到2006时对应的指头是__________________ (填出指头的名称,各指头的名称从上到下依次为大拇指、食指、中指、无名指、小指).
17.如图,△OAP、△ABQ均是等腰直角三角形,点P、Q在函数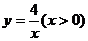 的图像上,直角顶点A、B均在
的图像上,直角顶点A、B均在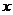 轴上,则点B的坐标为__________________ 。(保留根号)
轴上,则点B的坐标为__________________ 。(保留根号)

三.解答题:本大题共7个小题,共57分.解答应写出文字说明。证明过程或演算步骤.
18.(本小题满分7分)
(1) 已知两个分式: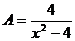 ,
,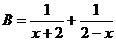 ,其中
,其中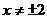 .下面有三个结论:
.下面有三个结论:
①A=B; ②A、B互为倒数; ③A、B互为相反数.通过计算得出正确结论.
(2) 解不等式组: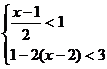
19.(本小题满分7分)
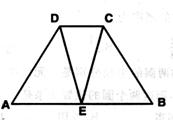
(1)已知:如图,梯形ABCD中,AB∥CD,AD=BC,E是底边AB的中点。
求证:DE=CE
(2)如图,在一次龙卷风中,一棵大树在离地面若干米处折断倒下,B为折断处最高点,树顶A落在离树根C的
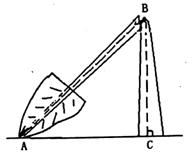
20.(本小题满分8分)
(1)解方程组:
(2)如图,一天早上,小张正向着教学楼AB走去,他发现教学楼后面有一水塔DC,可过了一会抬头一看:“怎么看不到水塔了?”心里很是纳闷。经过了解,教学楼、水塔的高分别为

21.(本小题满分8分)
田忌赛马是一个为人熟知的故事,传说战国时期,齐王与田忌各有上、中、下三匹马,同等级的马中,齐王的马比田忌的马强.有一天,齐王要与田忌赛马,双方约定:比赛三局,每局各出一匹,每匹马赛一次,赢得两局者为胜.看样子田忌似乎没有什么胜的希望,但是田忌的谋士了解到主人的上、中等马分别比齐王的中、下等马要强……
(1)如果齐王将马按上中下的顺序出阵比赛。那么田忌的马如何出阵,田忌才能取胜?
(2)如果齐王将马按上中下的顺序出阵,而田忌的马随机出阵比赛,田忌获胜的概率是多少?(要求写出双方对阵的所有情况)
22.(本小题满分9分)
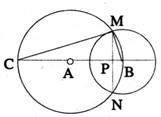
如图,BC是⊙A的直径,以B为圆心的圆与⊙A交于M、N两点,MN交BC于点P,
(1)说出CM与⊙B的位置关系,并简要说明理由;
(2)若⊙A的半径为2,⊙B的半径为1,求CM和MN的长。
23.(本小题满分9分)
已知⊙T与坐标轴有四个不同的交点M、P、N、Q,其中P是直线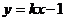 与
与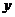 轴的交点。点Q与点P关于原点对称。抛物线
轴的交点。点Q与点P关于原点对称。抛物线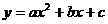 经过点M、P、N,其顶点为H。
经过点M、P、N,其顶点为H。
(1)求Q点的坐标;
(2)指出圆心T一定在哪一条直线上运动;
(3)当点H在直线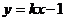 上.且⊙T的半径等于圆心T到原点距离的
上.且⊙T的半径等于圆心T到原点距离的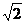 倍时,你能确定
倍时,你能确定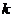 的值吗?若能,请求出
的值吗?若能,请求出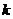 的值;若不能,请你说明理由。(第23题图供分析参考用,可能出现两种情况)
的值;若不能,请你说明理由。(第23题图供分析参考用,可能出现两种情况)

24.(本小题满分9分)
在Rt△ABC中,∠C=90°,∠A=60°,BC=6,等边△DEF从初始位置(点E与点B重合,EF落在BC上,如图1所示)在线段BC上沿BC方向以每秒1个单位的速度平移,DE、DF分别与AB相交于点M、N。当点F运动到点C时,△DEF终止运动,此时点D恰好落在AB上,设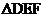 平移的时间为
平移的时间为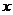 .
.
(1)求△DEF的边长;
(2)求M点、N点在BA上的移动速度;
(3)在△DEF开始运动的同时,如果点P以每秒2个单位的速度从D点出发沿DE→EF运动,最终运动到F点.若设△PMN的面积为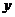 ,求
,求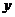 与
与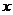 的函数关系式,写出它的定义域;并说明当P点在何处时,△PMN的面积最大?
的函数关系式,写出它的定义域;并说明当P点在何处时,△PMN的面积最大?
