2007年济南市天桥区九年级升学模拟考试
数学试卷(A卷)
本试卷分第I卷(选择题)和第II卷(非选择题)两部分。共120分。考试时间120分钟。
第I卷(选择题共48分)
注意事项:
1.数学考试允许使用不含有存储功能的计算器。
2.答第I卷前,考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上。
3.选择题为四选一题目,每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案,不能答在试卷上。
4.考试结束,监考教师将本试卷和答题卡一并收回。
一、选择题:(本大题共12小题,每小题4分,共48分。在每小题给出的四个选项中,只有一项符合题目要求)
1.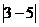 的值是
的值是
A.2 B.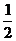 D.
D.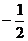
2.方程 的解是
的解是
A. B.
B.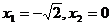
C.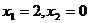 D.
D.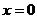
3.小虎在下面的计算中只做对了一道题,他做对的题目是
A.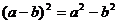 B.
B.
C.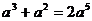 D.
D.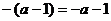
4.同时抛掷两枚均匀的硬币,则两枚硬币正面都向上的概率是
A. B.
B.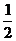 C.
C. D.1
D.1
5.已知反比例函数 的图像在第二、四象限,则
的图像在第二、四象限,则 的取值范围是
的取值范围是
A.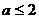 B.
B. C.
C.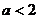 D.
D.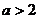
6.已知两个分式 ,
, ,其中
,其中 。则下面三个结论正确的是
。则下面三个结论正确的是
A.A=B B.A、B互为倒数
C.A、B互为相反数 D.以上结论均不正确
7.如图,DE是△ABC的中位线,则△ADE与△ABC的面积之比是
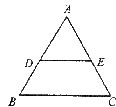
A.1∶1 B.1∶2 C.1∶3 D.1∶4
8.如图甲是某组合体的三视图,它们对应的组合体是图乙中的
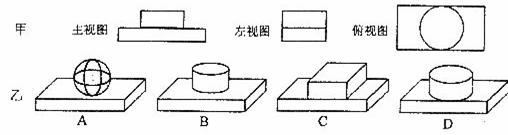
9.二次函数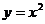 的图像向上平移2个单位,得到新的图像的二次函数表达式是
的图像向上平移2个单位,得到新的图像的二次函数表达式是
A. B.
B.
C.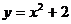 D.
D.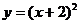
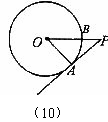
10.如图,PA为⊙O的切线,A为切点,PO交于⊙O点B,PA=4,OA=3,则cos∠APO的值为
A. B.
B.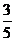 C.
C.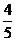 D.
D.



11.如图,已知点A的坐标为(1,0),点B在直线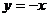 上运动,当线段AB最短时,点B的坐标为
上运动,当线段AB最短时,点B的坐标为
A. B.
B.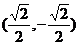
C.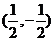 D.
D.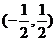
12.如图,在平行四边形ABCD中,对角线AC、BD相交于点O,F,E是对角线AC上的两点,当E,F满足下列哪个条件时,四边形DEBF不一定是平行四边形

A.OE=OF B.DE=BF
C.∠ADE=∠CBF D.∠ABE =∠CDF
第Ⅱ卷(非选择题,共72分)
注意事项:
1.第II卷共5页,用蓝、黑钢笔或圆珠笔直接答在试卷上。
2.答卷前将密封线内的项目填写清楚。
二、填空题:(本大题共5小题,每小题3分,共15分,把答案填写在题中横线上)
13.分解因式: 。
。
14.如图是一组数据的折线统计图,这组数据的极差和方差分别是 。



15.如图,将三角板的直角顶点放置在直线AB上的点O处,使斜边CD∥AB。则 的正切值为
。
的正切值为
。
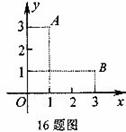
16.如图,已知点A的坐标为(1, 3),点B的坐标为(3, 1)。写出一个图像经过A、B两点的函数表达式 。

17.如图,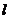 是四边形ABCD的对称轴,如果AD∥BC,则有以下结论:
是四边形ABCD的对称轴,如果AD∥BC,则有以下结论:
①AB∥CD ②AB=BC ③AB⊥BC ④AO=CO。那么其中正确的结论序号是 。
三、解答题:(本大题共7小题,共57分,解答应写出文字说明,证明过程或演算步骤)
18.(本小题满分7分)解下列不等式组和方程:
(1)解不等式组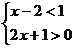
(2)解方程:
19.(本小题满分7分)完成下列各题:
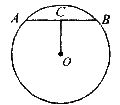
(1)如图,⊙O的半径为6,弦AB的长为8,求圆心O到弦AB的距离OC的长。
(2)已知:如图,E、F是四边形ABCD的对角线AC上的两点,AF=CE,DF=BE,DF//BE.
求证:四边形ABCD是平行四边形。

20.(本小题满分8分)经营户小王在蔬菜批发市场上了解到以下信息内容:
蔬菜品种
红辣椒
黄瓜
西红柿
茄子
批发价(元/公斤)
4
1.2
1.6
1.1
零售价(元/公斤)
5
1.4
2.0
1.3
他共用116元钱从市场上批发了红辣椒和西红柿共44公斤到菜市场去卖,当天卖完。请你计算出小王能赚多少钱?
21.(本小题满分8分)某社区从不同住宅楼中随机选取了200名居民,调查社区居民双休日的学习状况,并将得到的数据制成扇形统计图(如图1)和频数分布直方图(如图2)。
22.(本小题满分9分)如图,在菱形ABCD中,∠A=60°,AB=4,E是边AB上一动点,过点E作EF⊥AB交AD的延长线于点F,交BD于点M。
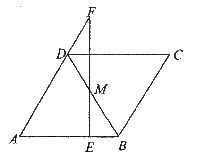
(1)请判断△DMF的形状,并说明理由。
(2)设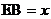 ,△DMF的面积为
,△DMF的面积为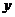 ,求
,求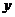 与
与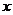 之间的函数关系式,并写出
之间的函数关系式,并写出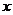 的取值范围。
的取值范围。
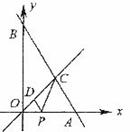 23.(本小题满分9分)如图,在平面直角坐标系中,直线
23.(本小题满分9分)如图,在平面直角坐标系中,直线 与
与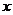 轴交于点A,与
轴交于点A,与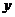 轴交于点B,与直线
轴交于点B,与直线 交于点C。
交于点C。
(1)求△OAC的面积;
(2)若P为线段OA(不含O,A两点)上的一个动点,过点P作PD∥AB交直线OC于点D,连结PC。设OP=t,△PDC的面积为S,求S与t之间的函数关系式;S是否存在最大值?如果存在,请求出来;如果不存在,请简要说明理由。
24.(本小题满分9分)矩形OABC在直角坐标系中的位置如图所示,A、C两点的坐标分别为A(6, 0)、C(0, 3),直线 与BC边相交于点D。
与BC边相交于点D。
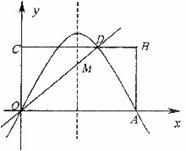
(1)求点D的坐标;
(2)若抛物线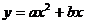 经过D、A两点,试确定此抛物线的表达式;
经过D、A两点,试确定此抛物线的表达式;
(3)设(2)中抛物线的对称轴与直线OD交于点M,点Q为对称轴上一动点,以Q、O、M为顶点的三角形与△OCD相似,求符合条件的Q点的坐标。