2006-2007学年度第二学期期中质量检测
八年级数学试题
时间:90分钟 分数:100分
一、选择题:(3分×10=30分)
1.己知分式 的值是零,那么
的值是零,那么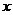 的值是( )
的值是( )
A. -1 B
2.若代数式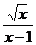 在实数范围内有意义,则
在实数范围内有意义,则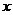 的取值范围为( )
的取值范围为( )
A.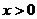 B.
B. C.
C.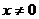 D.
D. 且
且
3.方程五 的根是( )
的根是( )
A.-3 B.
4.在平面直角坐标系中,点P(-3,5)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.是正比例函数 ,且
,且 随
随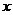 的值的增大而减小的图象是( )
的值的增大而减小的图象是( )

6.计算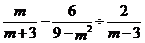 的结果为( )
的结果为( )
A.1 B.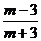 C.
C.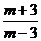 D.
D.
7.如图,已知∠1=∠2,AC=AD,增加下列条件:
①AB=AE;②BC=ED;③∠C=∠D;④∠B=∠E.

其中能使△ABC≌△AED的条件有( )
A.4个 B.3个 C.2个 D.1个
8.如果分式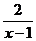 与
与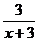 的值相等,则
的值相等,则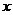 的值是(
)
的值是(
)
A.9 B.
9.如果两点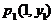 和
和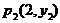 都在反比例函数
都在反比例函数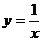 的图象上,那么( )
的图象上,那么( )
A.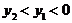 B.
B.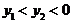 C.
C. D.
D. 
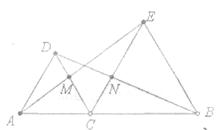
10.如图,△DAC和△EBC均是等边三角形,AE、BD分别与CD、CE交与点M、N,有如下结论:①△ACE≌△DCB;②CM=CN;③AC=DN.其中,正确结论的个数是( )
A.3个 B.2个 C.1个 D.0个
二、填空题(3分×10=30分)
11.已知空气的密度为
12.反比例函数的图象过点(-1,2),那么它的解析式为_____________.
13.点P1(a,b)和点P2(b,―1)关于 轴对称,那么a=________,b=_______.
轴对称,那么a=________,b=_______.
14.计算: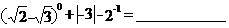 .
.
15.在函数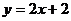 的图像中,与
的图像中,与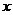 轴的交点坐标是_______________,与
轴的交点坐标是_______________,与 轴的交点坐标是______________,并且当
轴的交点坐标是______________,并且当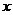 _________时,
_________时,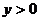 .
.
16.化简: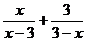 的结果是________________________.
的结果是________________________.
17.在平面直角坐标系中,点M(t-3,5-t)在x轴上,则t=______________.
18.如果 ,则
,则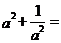 _______________.
_______________.
19.如下图,直线L过正方形ABCD的顶点B,点A、C到直线L的距离分别是1和2,则正方形的边长是____________________.

20.如图,AB=CD,AD、BC相交于点O,要使△ABO≌△DCO,应添加的条件是______.

三、解答题(5分×2=10分)
21.化简求值: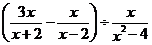 ,其中
,其中
22.矩形的周长是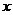 cm,另一边长为
cm,另一边长为 cm.
cm.
(1)求 关于
关于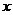 的函数关系式,并写出自变量
的函数关系式,并写出自变量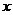 的取值范围;
的取值范围;
(2)在图中作出函数图像.

四、说理题(6分)
23.已知:如图,AB∥DE,且AB=DE.
(1)请你只添加一个条件,使△ABC≌△DEF,你添加的条件是________________.
(2)添加条件后,证明△ABC≌△DEF.
五、应用题(6分×3=18分)
24.某环保器材公司销售一种市场需求较大的新型产品,已知每件产品的进价为40元,经销过程中测出销售量 (万件)与销售单价
(万件)与销售单价 (元)存在如图所示的一次函数关系.
(元)存在如图所示的一次函数关系.

(1)求 关于
关于 的函数关系式;
的函数关系式;
(2)当销售量超过多少万件时公司将会赔本?
25.为了完善城市交通网络,方便市民出行,市政府决定修建东宝山交通隧道.现要使工程提前3个月完成,需将原定工作效率提高12%,求原计划完成这项工程需用多少个月?
26.近阶段国际石油价格猛涨,中国也受其影响.为降低运行成本,部分出租车公司将出租车由使用汽油改装为使用液化气.假设一辆出租车日平均行程为300千米.
(1)使用汽油的出租车,当前的汽油价格为4.6元/升.假设每升汽油能行驶12千米,行驶t天所耗的汽油费用为w元,请写出w关于t的函数关系式;
(2)使用液化气的出租车,当前的液化气价格为4.95元/千克.假设每千克液化气能行驶15千米,行驶t天所耗的液化气费用为P元,请写出P关于t的函数关系式;
(3)若出租车要改装为使用液化气,每辆需配置成本为8000元的设备.根据近阶段汽油和液化气的价位,在(1)、(2)的基础上,问需要几天才能收回改装成本?
六、探究题(6分)
27.如图,直角坐标系中,点A的坐标为(1,0),以线段OA为边在第四象限内作等边△AOB,点C为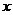 正半轴上一动点(OC>1),连结BC,以线段BC为边在第四象限内作等边△CBD,直线DA交
正半轴上一动点(OC>1),连结BC,以线段BC为边在第四象限内作等边△CBD,直线DA交 轴于点E.
轴于点E.

(1)△OBC与△ABD全等吗?判断并证明你的结论;
(2)随着点C位置的变化,点E的位置是否会发生变化?
若没有变化,求出点E的坐标;
若有变化,请说明理由.