2006-2007学年滨州市中考模拟试题(二)
数学试卷
本试题分第Ⅰ卷和第Ⅱ卷两部分.第Ⅰ卷为选择题.共30分;第Ⅱ卷为非选择题.共90分.满分为120分.考试时间为120分钟.
第Ⅰ卷 (选择题共30分)
一、选择题:本大题共10 小题.共30分.每小题所给出的四个答案选项中.有且只有一个是正确的.请把正确的选出来.每小题选对得3分.选错、不选或选出的答案超过一个。均记0分.
1.长江三峡水电站的总装机容量是18 200 000KW,用科学记数法表示为
(A) KW (B)
KW (B)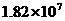 KW
KW
(C) KW (D)
KW (D)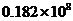 KW
KW
2.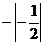 的倒数是
的倒数是
(A)2 (B)―2
(C)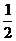 (D)
(D)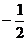
3.某鞋店在过去的一周中试销一种新款鞋,销售情况如下表所示:
型 号
22
22.5
23
23.5
24
24.5
25
销量(双)
3
5
10
15
8
4
2
对该店主来说,他最关注的数据是
(A)平均数 (B)众数
(C)中位数 (D)极差
4.下列运算正确的是
(A) (B)
(B)
(C)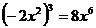 (D)
(D)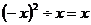
5.右图是由小立方块搭成的几何体的俯视图,小正方形中的数字是该位置的小立方块的个数,那么这个几何体的主视图是
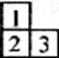

6.在一个不透明的口袋里有红白黑球共40个,这些球除颜色不同外其余都相同,如果从口袋中摸到红球的概率稳定在15%,摸到白球的概率稳定在45%,那么口袋中的黑球数为
(A)16个 (B)18个
(C)6个 (D)24个
7.不等式组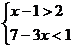 的解集是
的解集是
(A)x>2 (B)2<x<3
(C)x>3 (D)无解
8.右图是一张边被裁直的白纸,把一边折叠后,BC、BD为折痕,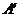 、
、 、B在同一直线上,则∠CBD的度数
、B在同一直线上,则∠CBD的度数
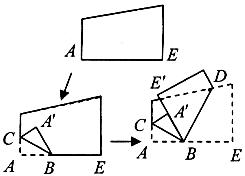
(A)不能确定 (B)大于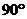
(C)小于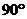 (D)等于
(D)等于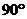
9.如图,用圆心角为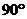 ,半径为8cm的扇形纸片恰好围成一个圆锥的侧面(忽略接缝),该圆锥底面圆的半径为
,半径为8cm的扇形纸片恰好围成一个圆锥的侧面(忽略接缝),该圆锥底面圆的半径为
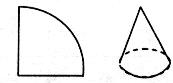
(A)4cm (B)3cm
(C)2cm (D)lcm
10.下列图形中,能判断∠1>∠2的是
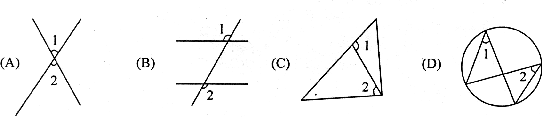
第Ⅱ卷 (非选择题共90分)
注意事项:
1.第Ⅱ卷共8页。使用蓝黑色钢笔或圆珠笔(作图除外).直接做在试卷上.
2.答卷前将密封线内的项目填写清楚.
二、填空题:本大题共8个小题,每小题3分.共24分.只要求填写最后结果,不写中间过程.
11.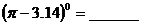 ;8的算术平方根是_______;
;8的算术平方根是_______; 。
。
12.化简: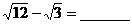 .
.
13.若关于x的一元二次方程 有实数根,则
有实数根,则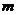 的取值范围是________.
的取值范围是________.
14.矩形ABCD的两条邻边的长分别为1和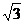 ,则其对角线的长为_________.
,则其对角线的长为_________.
15.如图,⊙O的直径CD过弦EF的中点,∠EOD=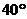 则∠DCF=________.
则∠DCF=________.

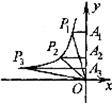
16.如图,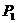 、
、 、
、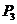 是双曲线上的三点,过这三点分别作y轴的垂线,得到三个三角形
是双曲线上的三点,过这三点分别作y轴的垂线,得到三个三角形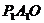 、
、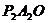 、
、 ,设它们的面积分别
,设它们的面积分别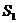 、
、 、
、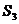 ;则
;则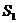 、
、 、
、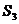 的大小关系是_______.
的大小关系是_______.
17.如图,在直角梯形ABCD中, ⊥BC,AD=1,BC=3,CD=4,EF为梯形的中位线,DH为梯形的高,则下列结论:
⊥BC,AD=1,BC=3,CD=4,EF为梯形的中位线,DH为梯形的高,则下列结论:

①∠BCD=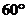 ;②四边形EHCF为菱形;
③
;②四边形EHCF为菱形;
③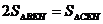 ;
;
④以AB为直径的圆与CD相切于点F,其中正确结论有_______个.
18.用黑白两种颜色的正方形纸片.摆出如下的图案.

白色纸片每次增加的个数是________;第(4)个图案的白色纸片共有________个;
第n个图案中的白色纸片共有_________个.
三、本大题共8个小题,共66分.解答要求写出文字说明、证明过程或推演步骤.
19.(本小题满分5分)请你先将分式 化简,再求出当a=9999时,该代数式的值.
化简,再求出当a=9999时,该代数式的值.
20.(本小题满分6分)某商场正在热销2008年北京奥运会吉祥物“福娃”玩具和徽章两种奥运商品,请你根据下图提供的信息,求一盒“福娃”和一枚徽章的价格各是多少元?


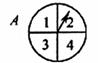
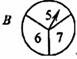
21.(本小题满分6分)如果有两个质地均匀的转盘A、B,转盘A被四等分,分别标有1、2、3、4;转盘B被三等分,分别标有5、6、7,小明与小强用这两个转盘玩游戏,约定规则如下:随机转动转盘各一次,停止后,将A、B转盘中指针所指的数字相乘,积为偶数小明赢,否则小强赢.
(1)约定的规则公平吗?通过计算说明:
(2)如果约定的规则不公平,谁赢的可能性较大?
请你只在转盘B中修改一个数字,使游戏公平.
22.(本小题满分6分)在方格纸(每个小方格都是边长为单位长度的正方形)中,我们称每个小正方形的顶点为格点,以格点为顶点的图形叫格点图形.如右图中的△ABC叫格点△ABC.
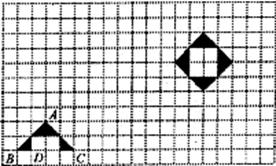
(1)如果A、D两点的坐标分别为(1,1)和(0,一1),请你在方格纸中建立平面直角坐标系,并直接写出B、C点的坐标:
(2)请根据你学过的平移、旋转或对称等知识,说明图中的“格点四边形”图案是怎样通过“格点△ABC”变换得到的?
23.(本小题满分9分)如图,在平行四边形ABCD中,E、F分别是AB、CD上的点,且∠DAF=∠BCE.
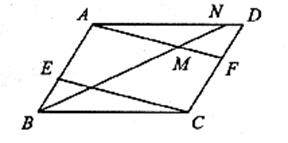
(1)求证:△DAF≌△BCE;
(2)若∠ABC=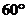 ,∠ECB=
,∠ECB= ,∠ABC的平分线BN交AF于M,交AD于N,求∠AMN的度数.
,∠ABC的平分线BN交AF于M,交AD于N,求∠AMN的度数.
24.(本小题满分10分)以下两图是某媒体公布的中国人口发展情况统计图和2000年中国人口年龄构成图,请根据图中提供的信息,回答以下问题:

(1)2000年,中国60岁及以上人口数为______亿,15~59岁人口数为________亿,(精确到0.01亿).
(2)预计到2050年,中国总人口数将达到_______亿,60岁及以上人口数占总人口数的____%(精确到0.1%).
(3)通过对中国人口发展情况统计图的分析,写出两条你认为正确的结论.
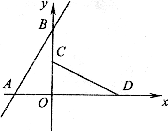
25.(本小题满分12分)如图,直线y=2x+4与x轴、y轴分别相交于A、B两点,把△OAB绕点O顺时针旋转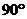 得到△OCD.
得到△OCD.
(1)求经过A、B、D三点的抛物线的解析式:
(2)在所求抛物线上是否存在点P,使得直线CP把△OCD分成面积相等的两部分?如果存在,求出点P的坐标:如果不存在,请说明理由.
26.(本小题满分12分)已知点P在线段4B上,点O在线段AB的延长线上,以点O为圆心,OP为半径作圆,点C是圆O上一点.
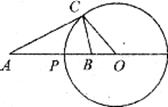
(1)如果AP=2PB,PB=BO.求证△CAO∽△BCO;
(2)如果AP=m(m是常数,且m>1),BP=1,OP是OA、OB的比例中项,当点C在圆周上运动时,求AC:BC的值(结果用含m的式子表示);
(3)在(2)的条件下,讨论以BC为半径的圆B和以CA为半径的圆C的位置关系,并写出相应的m的取值范围.