2006年莱芜市中等学校招生考试数学试题
注意事项:
1.答卷前考生务必在规定的位置将姓名、准考证号等内容填写准确。
2.本试卷分第Ⅰ卷和第Ⅱ卷两部分。第Ⅰ卷为选择题,42分;第Ⅱ卷为非选择题,78分,共120分。考试时间为120分钟。
3.请将第Ⅰ卷选择题答案填写在第Ⅱ卷卷首答案栏内,填在其他位置不得分。
4.考试结束后,由监考教师把第Ⅰ卷和第Ⅱ卷一并收回。
第Ⅰ卷(选择题42分)
一、选择题(本大题共14小题,在每小题给出的四个选项中,只有一项是正确的,请把正确的选项填在答案栏的相应位置上.选错、不选或多选均不得分,每小题3分,共42分)
1. 的绝对值是
的绝对值是
A.-3 B. C.3 D.
C.3 D.
2.下列计算正确的是
A.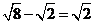 B.
B.
C.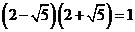 D.
D.
3.若反比例函数 的图像经过点(-1,2),则这个函数的图像一定经过点
的图像经过点(-1,2),则这个函数的图像一定经过点
A.(2,-1) B.(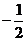 ,2) C.(-2,-1) D.(
,2) C.(-2,-1) D.(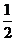 ,2)
,2)
4.钟表的轴心到分针针端的长为
A. cm B.
cm B.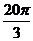 cm C.
cm C.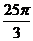 cm D.
cm D.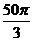 cm
cm
5.已知方程组 的解为
的解为 ,则
,则
A.4 B.
6.若方程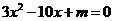 有两个同号不等的实数根,则优的取值范围是
有两个同号不等的实数根,则优的取值范围是
A.m≥0 B.m> D.0<m≤
D.0<m≤
7.如图所示:边长分别为l和2的两个正方形,其一边在同一水平线上,小正方形沿该水平线自左向右匀速穿过大正方形.设穿过的时间为t,大正方形内除去小正方形部分的面积为S(阴影部分),那么S与t的大致图象应为


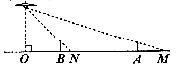 8.加图.路灯距地面
8.加图.路灯距地面
A.变长3.
C.变短3.
9.某市出租车的收费标准是:起步价为5元(即行驶距离不超过
 A.
A.
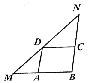
10.在△MBN中,BM=6,点爿、C、D分别在MB、NB、MN上,四边形ABCD为平行四边形,∠NDC=∠MDA,平行四边形ABCD的周长是
A.24 B.
 11.如图,已知在矩形ABCD中,E、F、G、H分别为AB、BC、CD、DA 的中点。若
11.如图,已知在矩形ABCD中,E、F、G、H分别为AB、BC、CD、DA 的中点。若 ,AE=5,则四边形EFGⅣ的面 积是
,AE=5,则四边形EFGⅣ的面 积是
A.240 B.
12.已知点A(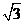 ,1),B(0,0),C(
,1),B(0,0),C(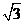 ,0),AE平分∠BAC,交BC于点E,则直线AE对应的函数表达式是
,0),AE平分∠BAC,交BC于点E,则直线AE对应的函数表达式是
A.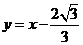 B.
B.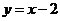 C.
C.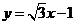 D.
D.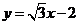
 13.已知等腰梯形的下底长为
13.已知等腰梯形的下底长为
A.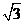 cm2 B.16
cm2 B.16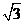 cm2 C.24
cm2 C.24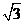 cm2 D.12cm2
cm2 D.12cm2
14.如图,点B是线段AC的中点,过点C的直线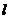 与AC成60°的角,在直线
与AC成60°的角,在直线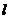 上取一点P,使得∠APB=30°,则满足条件的点P的个数是
上取一点P,使得∠APB=30°,则满足条件的点P的个数是
A.3个 B.2个 C.1个 D.不存在
第Ⅱ卷(非选择题78分)
注意事项:
第Ⅱ卷共6页,用钢笔或圆珠笔直接答在本试卷上。
二、填空题(每小题3分,共15分)
15.随着我国综合国力的提升,近年来全球学习汉语的人数不断增加.据报道,2005年海外学习汉语的人数已达38 200 000人,用科学记数法表示为 人。
16.因式分解: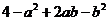 =
=
17.计算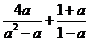 的结果是
.
的结果是
.
18.要在一个矩形纸片上画出半径分别是4cm和lcm的两个相外切的圆,该矩形面积的最小值是 .
19.已知:△ABC中,AB=a.
如图(1),若A1、B1,分别是CA、CB的中点,则A1B1=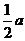 ;
;
如图(2),若A1、A2 ,B1、B2分别是CA、CB的三等分点,则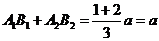
如图(3),若A1、A2 、A3,B1、B2、B3分别是CA、CB的四等分点,
则A1 B1+ A2
B2+ A3 B3=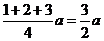 ;
;
如图(4),若A1、A2 ……A9,B1、B2……B9,分别是CA、CB的十等分点,
则A1 B1+ A2 B2+…+A9B9=

三、解答题:(本大题共7小题,共63分.解答要写出必要的文字说明、证明过程或推演步骤.)
20.(7分)解不等式组,并把其解集在数轴上表示出来:

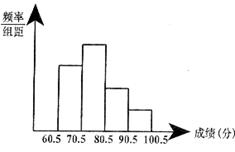
21.(7分)某中学举行了数学竞赛选拔赛,数学老师将所有参赛学生的成绩(分数均为整数,满分100分)进行了统计,并绘制了频率分布直方图,如图所示:
(1)请你依据频率分布直方图写出两条正确的信息;
(2)参赛人数为20人,这四个小组频率的比为3:4:2:1.
 ①规定成绩高于80分的为优秀,求参赛学生成绩的优秀率.
①规定成绩高于80分的为优秀,求参赛学生成绩的优秀率.
②求所有参赛学生的平均分 的范围.
的范围.
22.(8分)近年来,由于受国际石油市场的影响,润滑油价格不断上涨.某种润滑油今年5月份的价格比去年5月份每桶多2元,客户小王用了120元钱购买这种润滑油,比去年5月份恰好少买2桶,问今年5月份这种润滑油每桶的价格是多少元?
 23.(9分)两个全等的含30°、60°角的三角板ADE和三角板ABC如图所示放置,E、A、C三点在同一条直线上,连结BD,取肋的中点M,连结ME,MC.试判断AEMC的形状,并说明理由.
23.(9分)两个全等的含30°、60°角的三角板ADE和三角板ABC如图所示放置,E、A、C三点在同一条直线上,连结BD,取肋的中点M,连结ME,MC.试判断AEMC的形状,并说明理由.
24.(10分)已知:关于x的二次函数y=-x2+(m+2)x-m.
(1)证明:不论m为任何实数,二次函数图像的顶点P总在x轴的上方;
(2)设二次函数图像与y轴交于点A,过点A做x轴的平行线与图像交于另外一点B.若顶点P在第一象限,当m为何值时,△PAB是等边三角形?
25.(10分)如图,在AABC中,AB=AC=1,点D、E在直线BC上运动.设BD=x,CE=Y.
(1)如果∠BAC=30º,∠DAE=105º,试确定y与x之间的函数关系式;
 (2)如果∠BAC的度数为α,∠DAE的度数为β,当α,β满足怎样的关系式时,(1)中y与X之间的函数关系式仍然成立,试说明理由.
(2)如果∠BAC的度数为α,∠DAE的度数为β,当α,β满足怎样的关系式时,(1)中y与X之间的函数关系式仍然成立,试说明理由.
26.(12分)半径为2.5的⊙O中,直径AB的不同侧有定点C和动点P.已知BC:CA=4:3,点P在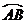 上运动,过点C作CP的垂线,与PB的延长线交于点Q .
上运动,过点C作CP的垂线,与PB的延长线交于点Q .
(1)当点P运动到与点C关于AB对称的位置时,求CQ的长;
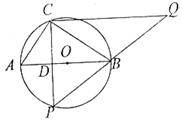

(2)当点P运动到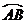 的中点时,求CQ的长;
的中点时,求CQ的长;
(3)当点P运动到什么位置时,CQ取到最大值,并求此时CQ的长.