2006年福建省福州市中考模拟试卷
一、选择题(本大题包括10小题,每小题3分,共30分,每小题只有一个正确答案)
1、下列各点中,在第三象限的点是 ( )
A.(2,4) B.(2,-4) C.(-2,4) D.(-2,-4))
2、0.002006用科学记数法表示为 ( )
3、一元二次方程x2-1=0的根为( )
A.x=1 B. x=
4、如图,已知圆心角∠BOC=100°,则圆周角∠BAC的度数为 ( )
 A.
100°
B. 130° C. 50° D. 80°
A.
100°
B. 130° C. 50° D. 80°
5、(a+b)( a-b)= ( )
A.
a2+b2
B. a2-b
6、圆锥的侧面展开图是( )
A.扇形 B.矩形 C.三角形 D.圆
7、不等式组 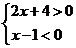 ( )
( )
A. x>1或x <-2 B. x>
8、右图是一个正方体包装盒的表面展开图,若在其中的三个正方形A、B、C内分别填上适当的数,使得将这个表面展开图沿虚线折成正方体后,相对面上的两个数互为相反数,则填在A、B、C内的三个数依次是 ( )
A.0,-2,1 B. 0,1,
9、下列形状的地砖中,不能把地面作既无缝隙又不重叠覆盖的地砖是 ( )
A.正三角形 B.正方形 C.正五边形 D.长方形
10、根据下图中的中的尺寸(AB∥A`B`),那么像长y(A`B`的长)与物长x(AB的长)之间函数关系的图象大致是( )
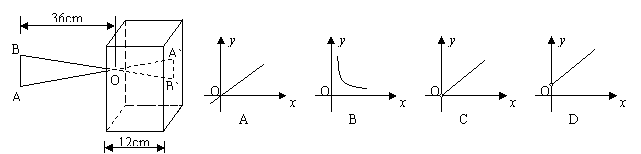 |
二、填空题(本题共5小题,每小题4分,共20分)
 11.5的算术平方根是______________
11.5的算术平方根是______________
12.一枚骰子,六面上的数字分别为1,2,3,4,5,6,投掷一次,向上的面出现数字3的概率是____________。
13.两个相似五边形的相似比为2∶3,则它们的面积比为____________。
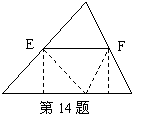
14.我们曾经像右图那样折叠一个三角形纸片,把三角形的三个角拼在一起,用这种方法我们可以证明定理“________________________”。在折叠过程中折痕EF是三角形的__________线。
15.用计算器探索:按一定规律排列的一组数:,,,…,,,如果从中选出若干个数,使它们的和大于0.5,那么至少要___________个数。
三、解答题
16.(本小题10分)先化简,再求值:+ -1,其中x=
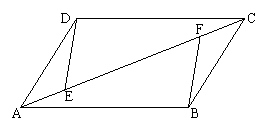
17、 (本小题10分)已知如图,AB=CD,BC=AD,E、F是AC上的两点,且AF=CE。
求证:△ABF≌△CDE。
18.(本小题10分)甲、乙两名运动员在6次百米跑训练中的成绩如下:(单位:s)
第一次
第二次
第三次
第四次
第五次
第六次
甲
10.8
10.9
11.0
10.7
11.2
10.8
乙
10.9
10.9
10.8
10.8
10.5
10.9
请你比较这两组数据中的众数、平均数、中位数、方差,谈谈你的看法。
19、(本小题10分)永盛电子有限公司向银行申请了甲乙两种贷款,共计68万元,每年需付出利息8.42 万元。甲种贷款每年的利率是12%,乙种贷款每年的利率是13%。求两种贷款的本金分别是多少?
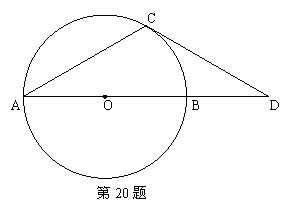
20、(本小题10分)如图AB是⊙O的直径,点D在AB的延长线上,且BD=OB,点C在⊙O上,且∠CAB=30°。求证:CD是⊙O的切线。
21、(本小题12分)池塘中竖着一块碑CD,在高于水面
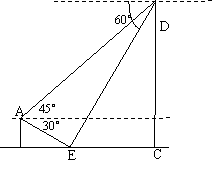 |
 22.
(本小题12分) 已知如图边长为2的正方形OABC的顶点A在x轴的正半轴上,将正方形OABC绕原点顺时针旋转30°,使点A落在双曲线y=(k<0)的图象上。
22.
(本小题12分) 已知如图边长为2的正方形OABC的顶点A在x轴的正半轴上,将正方形OABC绕原点顺时针旋转30°,使点A落在双曲线y=(k<0)的图象上。
(1)求双曲线y=的函数关系式。
(2)正方形OABC继续按顺时针旋转一周,当旋转多少度时,点A会再次落在双曲线y=的图象上?并求出此时点A的坐标。
23. (本小题12分)你能设计一个方案把一张正方形的纸用剪刀一次剪出4个正方形吗?(可以把纸折叠)并简要说明理由
 |
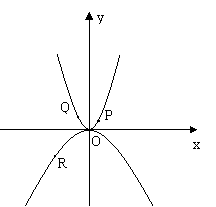
24、如图,两条抛物线的解析式分别为y=3x2与y=-x2,P、Q两点在y=3x2上,P点的横坐标为,Q点的横坐标为-1,R点在y=-x2上,R点的横坐标为-2。
(1)对于函数y=-x2,当-3≤x≤4时,求y的取值范围。
(2)求△QRO与△QOP面积的比。
(3)过R点作直线RM∥x轴,交抛物线y=-x2于点M,在抛物线y=-x2上是否存在点A,在y轴上有一点B,使R、M、A、B为顶点的四边形为平行四边形。若存在求出点A、B的坐标和平行四边形的面积;若不存在,请说明理由。
 |