2003年山东省烟台市初中毕业、升学统一考试
第一卷
一、选择题(本题共15个小题,每小题3分.共计45分).每小题都给出标号为A、B、C、
D四个备选答案,其中有且只有一个是正确的.
1.下列各数中,负数是( )
(A)-(-3) (B)-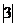 (C)
(C)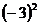 (D)-
(D)-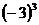
2.不等式ax>b的解集是x<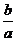 ,那么a的取值范围是(
)
,那么a的取值范围是(
)
(A)a≤0 (B)a<0 (C)a≥0 (D)a>0
3.若a>0,b<-2,则点(a,b+2)应在( )
(A)第一象限 (B)第二象限 (C)第三象限 (D)第四象限
4. 若3x-2y=0,则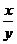 等于( )
等于( )
(A)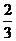 (B)
(B)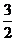 (C)
(C)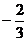 (D)
(D)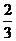 或无意义
或无意义
5.若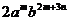 与
与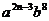 的和仍是一个单项式,则m与n的值分别是( )
的和仍是一个单项式,则m与n的值分别是( )
(A)1,2(B)2,1(C)1,1(D)1,3
6.已知一个凸四边形ABCD的四条边的长顺次是a、b、c,d,且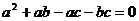 ,
,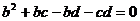 ,那么四边形ABCD是(
)
,那么四边形ABCD是(
)
(A)平行四边形 (B)矩形 (C)菱形 (D)梯形
7.已知x为实数,且 ,那么
,那么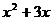 的值为( )
的值为( )
(A)1 (B)-3或1 (C)3 (D)-1或3
8.某学生用一架不等臂天平称药品.第一次将左盘放入50克砝码,右盘放药品使天平平衡.第二次将右盘放入50克砝码,左盘放药品使天平平衡.则两次称得药品的质量和( )
(A)等于100克
(B)大于100克
(C)小于100克
(D)以上情况都有可能
9. 若ab<o,则代数式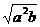 可化简为( )
可化简为( )
(A)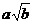 (B)
(B)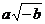 (C)
(C)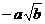 (D)
(D)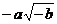
10.从边长为1的等边三角形内一点分别向三边作垂线,三条垂线段长的和为( )
(A)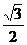 (B)
(B)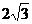 (C)
(C)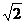 (D)
(D)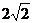
11.开发区某消毒液生产厂家自2003年初以来,在库存为m(m>0)的情况下,日销售量与产量持平,自4月底抗“非典”以来,消毒液需求量猛增,在生产能力不变的情况下,消毒液一度脱销,以下表示2003年初至脱销期间,时间t与库存量y之间函数关系的图像是( )
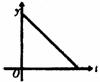

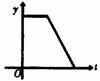
(A)
(B)
(C)
(D)
12.如图,△ABC中,AD⊥BC于D,BE⊥AC于E,AD与BE相交于F,若BF=AC,那么∠ABC的大小是( )
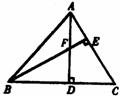
(A)40°
(B)45° (C)50° (D)60°
13.对于方程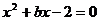 ,下面观点正确的是( )
,下面观点正确的是( )
(A)方程有无实数根,要根据b的取值而定
(B)无论b取何值,方程必有一正根、一负根
(C)当b>0时.方程两根为正:b<0时.方程两根为负
(D)∵ -2<0,∴ 方程两根肯定为负
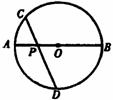
14.如图,P是直径AB上一点,且PA=2cm,PB=6cm,CD为A过P点的弦,那么下列PC与PD的长度中.符合题意的是( )
(A)1cm,12cm (B)3cm.5cm (C)7cm,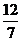 cm (D)3cm.4cm
cm (D)3cm.4cm
15.一块等边三角形的木板,边长为1,现将木板沿水平线翻滚(如图),那么B点从开始至结束所走过的路径长度为( )
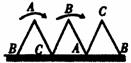
(A)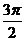 (B)
(B)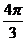 (C)4 (D)2+
(C)4 (D)2+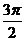
第二卷
二、填空题(本题共5个小题,每小题3分,共计15分)
16.函数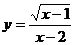 的自变量x的取值范围是 。
的自变量x的取值范围是 。
17.今年6月10日三峡库区蓄水水位达到135米,整个三峡工程约有112.6万移民,其中该水位以下移民约占36.7%,那么该水位以下共搬迁约 人.(保留三位有效数字)
18.从甲、乙、丙三个厂家生产的同一种产品中各抽取8件产品,对其中使用寿命跟踪调查.结果如下:(单位:年)
甲:3,4,5,6,8,8,8,10
乙:4,6,6,6,8,9,12,13
丙:3,3,4,7,9,10,11,12
三个厂家在广告中都称该产品的使用寿命是8年,请根据结果判断厂家在广告中分别运用了平均数、众数、中位数中的哪一种集中趋势的特征数:甲 ,乙 ,丙 。
19.升国旗时,某同学站在离旗杆底部24米处行注目礼,当国旗升至旗杆顶端时,该同学视线的仰角恰为30°.若双眼离地面1.5米.则旗杆高度为 米〔用含根号的式子表示〕.
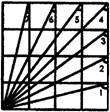
20.在如图所示的4x4正方形网格中.∠1+∠2+∠3+∠4+∠5+∠6+∠7=
。
三、(本题共3个小题,第21小题6分,第22小题8分,第23小题8分,共计22分)
21.细心观察图形,认真分析各式,然后解答问题。
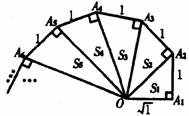
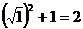
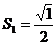
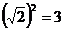
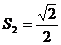
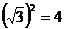
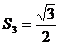
……
……
(1)请用含有n(n是正整数)的等式表示上述变化规律.
(2)推算出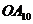 的长.
的长.
(3)求出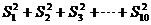 的值.
的值.
22.设 a、b、c都是实数,且满足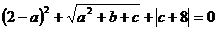 ,
,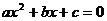 。求代数式
。求代数式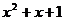 的值.
的值.
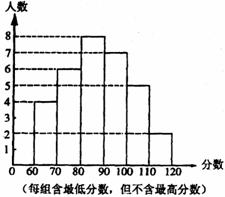
23.某中学部分同学参加全国初中数学竞赛,取得了优异的成绩.指导老师统计了所有参赛同学的成绩(成绩都是整数,试题满分120分),并且绘制了“频率分布直方图”(如图).
请回答:
(1)该中学参加本次数学竞赛的有多少名同学?
(2)如果成绩在90分以上(含90分)的同学获奖,那么该中学参赛同学的获奖率是多少?
(3)这次竞赛成绩的中位数落在哪个分数段内?
(4)图中还提供了其它信息,例如该中学没有获得满分的同学等等.请再写出两条信息.
四、(本题满分8分)
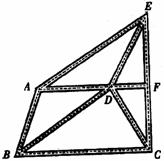
24.如图,是某城市部分街道示意图,AF∥BC,EC⊥BC,BA∥DE.BD∥AE.甲、乙两人同时从B站乘车到F站.甲乘1路车.路线是B-A-E-F;乙乘2路车,路线是B-D-C-F.假设两车速度相同,途中耽误时间相同,那么谁先到达F站.请说明理由.
五、(本题满分10分)
25.如图,AB为半圆的直径,O为圆心,AB=6,延长BA到F,使FA=AB,若P为线段AF上的一个动点(不与A重合),过P点作半圆的切线,切点为C,过B点作 BE⊥PC交PC的延长线于E.设AC=x,AC+BE=y,求y与 x的函数关系式及x的取值范围.

六、(本题满分8分)
26.烟台大樱桃闻名全国,今年又喜获丰收,某大型超市从大樱桃生产基地购进一批大樱桃,运输过程中质量损失5%.(超市不负责其它费用)
(1)如果超市把售价在进价的基础上提高5%,超市是否亏本?通过计算说明.
(2)如果超市要获得至少20%的利润,那么大樱桃售价最低应提高百分之几?(结果精确到0.1%)
七、(本题满分10分)
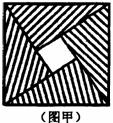
27.(1)四年一度的国际数学家大会于2002年8月20日在北京召开.大会会标如图甲.它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形.若大正方形的面积为13,每个直角三角形两直角边的和是5.求中间小正方形的面积.
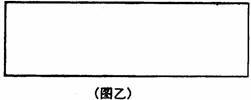
(2)现有一张长为6.5cm、宽为2cm的纸片,如图,请你将它分割成6块,再拼合成一个正方形.(要求:先在图乙中画出分割线,再画出拼成的正方形并标明相应数据)
八、(本题满分8分)
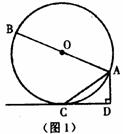
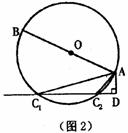
29.如图1,AB是⊙O的直径,AC是弦,直线CD切⊙O于点C.AD⊥CD,垂足为D.
(1)求证: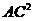 =AB?AD
=AB?AD
(2)若将直线CD向上平移,交⊙O于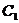 、
、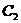 两点,其它条件不变,可得到图2所示的图形,试探索A
两点,其它条件不变,可得到图2所示的图形,试探索A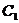 、A
、A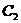 、AB、AD之间的关系,并说明理由.
、AB、AD之间的关系,并说明理由.
(3)把直线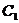 D继续向上平移,使弦
D继续向上平移,使弦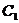
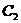 与直径AB相交(交点不与A、B重合),其它条件不变.请你在图3中画出变化后的图形,标好相应字母,并试着写出与(2)相应的结论,判断你的结论是否成立?若不成立,请说明理由;若成立,请给出证明.
与直径AB相交(交点不与A、B重合),其它条件不变.请你在图3中画出变化后的图形,标好相应字母,并试着写出与(2)相应的结论,判断你的结论是否成立?若不成立,请说明理由;若成立,请给出证明.

十、(本题满分12分)
30. 在直角坐标系中,有以A(-1,-1),B(1,-1),C(1,1),D(-1,1)为顶点的正方形.设正方形在直线y=x上方及直线y=-x+2a上方部分的面积为S.
(1)求a=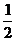 时,S的值.
时,S的值.
(2)当a在实数范围内变化时,求S关于a的函数关系式.