1. 绝对值为4的实数是   (    )

A. ±4              B. 4       C. －4              D. 2

2. 对x²-3x+2分解因式，结果为 (     )

A. x(x-3)+2         B. (x-1)(x-2)           C. (x-1)(x+2)           D. (x+1)(x-2)

3. 若a为任意实数，则下列等式中恒成立的是 (     )

A. a+a=a²            B. a×a=2a          C. 3a³－2a²=a            D. 2a×3a²=6a³

4. 已知小明同学身高1.5米，经太阳光照射，在地面的影长为2米，若此时测得一塔在同一地面的影长为60米，则塔高应为 (     )

A. 90米             B. 80米             C. 45米             D. 40米

5. 化简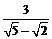时，甲的解法是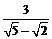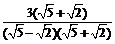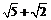：==，乙的解法是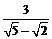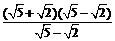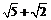：==，以下判断正确的是 (     )

A. 甲的解法正确，乙的解法不正确         B. 甲的解法不正确，乙的解法正确

C. 甲、乙的解法都正确                     D. 甲、乙的解法都不正确

6. 如果关于x的不等式 (a+1) x>a+1的解集为x<1，那么a的取值范围是  (     )

A. a>0              B. a<0              C. a>-1             D. a<-1

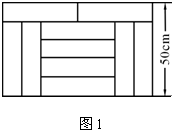7. 如图1，宽为50 cm的矩形图案由10个全等的小长方形拼成，其中一个小长方形的面积为  (     )

A. 400 cm²                       B. 500 cm²

C. 600 cm²                       D. 4000 cm²

8. 点M(－sin60°，cos60°)关于x轴对称的点的坐标是  (     )

A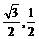．()                  B．(－)

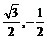C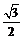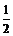．(－,)                   D．(－,-)

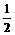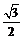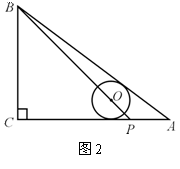
9. 如图2，在ΔABC中，∠C=90°，AC=8，AB=10，点P在AC上，AP=2，若⊙O的圆心在线段BP上，且⊙O与AB、AC都相切，则⊙O的半径是  (     )

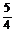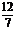A. 1            B.                C.                    D.

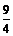
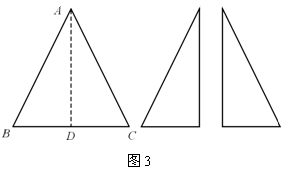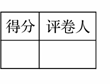
10. 如图3，已知BC为等腰三角形纸片ABC的底边，AD⊥BC，AD=BC. 将此三角形纸片沿AD剪开，得到两个三角形，若把这两个三角形拼成一个平面四边形，则能拼出互不全等的四边形的个数是 (     )

A. 1                    B. 2

C. 3                    D. 4

11. 若正比例函数y=mx (m≠0)和反比例函数y=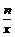 (n≠0)的图象都经过点(2,3)，则m=______，n=_________ .

12. 如图4，在ΔABC中，BC=5 cm，BP、CP分别是∠ABC和∠ACB的角平分线，且PD∥AB，PE∥AC，则ΔPDE的周长是___________ cm.

13. 若非零实数a,b满足4a²+b²=4ab，则=___________.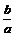

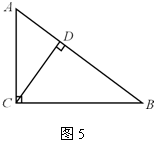
14. 如图5，若CD是RtΔABC斜边上的高，AD=3，CD=4，则BC=__________ .

15. 我市某县城为鼓励居民节约用水，对自来水用户按分段计费方式收取水费：若每月用水不超过7立方米，则按每立方米1元收费；若每月用水超过7立方米，则超过部分按每立方米2元收费. 如果某居民户今年5月缴纳了17元水费，那么这户居民今年5月的用水量为________立方米 .

16. 分析图6①,②,④中阴影部分的分布规律，按此规律在图6③中画出其中的阴影部分.

三. 解答题：本大题共8个小题，共52分. 解答应写出必要的文字说明,证明过程或演算步骤.

17 (本小题满分5分)

请你用三角板、圆规或量角器等工具，画∠POQ=60°，在它的边OP上截取OA=50 mm，OQ上截取OB=70 mm，连结AB，画∠AOB的平分线与AB交于点C，并量出AC和OC 的长 .

(结果精确到1 mm，不要求写作法).

18 (本小题满分6分)

已知等式 (2A-7B) x+(3A-8B)=8x+10对一切实数x都成立，求A、B的值.

19 (本小题满分6分)

我市部分学生参加了2004年全国初中数学竞赛决赛，并取得优异成绩. 已知竞赛成绩分数都是整数，试题满分为140分，参赛学生的成绩分数分布情况如下：

分数段

0－19

20－39

40－59

60－79

80－99

100－119

120－140

人  数

0

37

68

95

56

32

12

请根据以上信息解答下列问题：

(1) 全市共有多少人参加本次数学竞赛决赛？最低分和最高分在什么分数范围？

(2) 经竞赛组委会评定，竞赛成绩在60分以上 (含60分)的考生均可获得不同等级的奖励，求我市参加本次竞赛决赛考生的获奖比例；

(3) 决赛成绩分数的中位数落在哪个分数段内？

(4) 上表还提供了其他信息，例如：“没获奖的人数为105人”等等. 请你再写出两条此表提供的信息.

20 (本小题满分6分)

已知实数a满足a²＋2a－8=0，求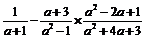的值.

21 (本小题满分6分)

已知关于x的方程 kx²-2 (k+1) x+k-1=0 有两个不相等的实数根，

(1) 求k的取值范围；

(2) 是否存在实数k，使此方程的两个实数根的倒数和等于0 ？若存在，求出k的值；若不存在，说明理由.

22 (本小题满分7分)

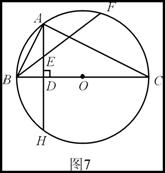如图7，已知BC是⊙O的直径，AH⊥BC，垂足为D，点A为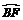的中点，BF交AD于点E，且BE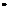EF=32，AD=6.

(1) 求证：AE=BE；

(2) 求DE的长；

(3) 求BD的长 .

23 (本小题满分8分)

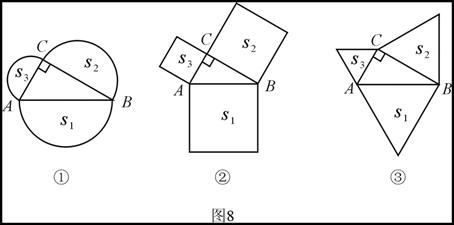
如图8①，分别以直角三角形ABC三边为直径向外作三个半圆，其面积分别用S₁、S₂、S₃表示，则不难证明S₁=S₂+S₃ .

(1) 如图8②，分别以直角三角形ABC三边为边向外作三个正方形，其面积分别用S₁、S₂、S₃表示，那么S₁、S₂、S₃之间有什么关系？(不必证明)

(2) 如图8③，分别以直角三角形ABC三边为边向外作三个正三角形，其面积分别用S₁、S₂、S₃表示，请你确定S₁、S₂、S₃之间的关系并加以证明；

(3) 若分别以直角三角形ABC三边为边向外作三个一般三角形，其面积分别用S₁、S₂、S₃表示，为使S₁、S₂、S₃之间仍具有与(2)相同的关系，所作三角形应满足什么条件？证明你的结论；

(4) 类比(1)、(2)、(3)的结论，请你总结出一个更具一般意义的结论 .

24 (本小题满分8分)

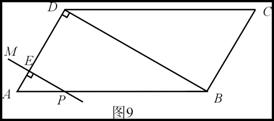
如图9，在平行四边形ABCD中，AD=4 cm，∠A=60°，BD⊥AD. 一动点P从A出发，以每秒1 cm的速度沿A→B→C的路线匀速运动，过点P作直线PM，使PM⊥AD .

(1) 当点P运动2秒时，设直线PM与AD相交于点E，求△APE的面积；

(2) 当点P运动2秒时，另一动点Q也从A出发沿A→B→C的路线运动，且在AB上以每秒1 cm的速度匀速运动，在BC上以每秒2 cm的速度匀速运动. 过Q作直线QN，使QN∥PM. 设点Q运动的时间为t秒(0≤t≤10)，直线PM与QN截平行四边形ABCD所得图形的面积为S cm² .

① 求S关于t的函数关系式；

② (附加题) 求S的最大值.

注：附加题满分4分，但全卷的得分不超过100分.