2005年潍坊市中等学校招生考试
第Ⅰ卷
一、选择题 (本题共12小题,共36分,在每小题给出的四个选项中,只有一个是正确的,请把正确的选项选出来.每小题选对得3分,选错、不选或选出的答案超过一个均记零分.)
1.今年在北京举行的“财富世界论坛”的有关资料显示,近几年中国和印度经济的年平均增长率分别为7.3%和6.5%,则近几年中国比印度经济的年平均增长率高( ).
A.0.8 B.0.08
C.0.8 % D.0.08%
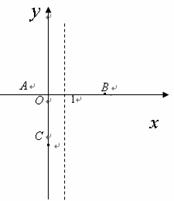
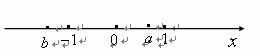
2.已知实数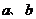 在数轴上对应的点如图所示,则下列式子正确的是( ).
在数轴上对应的点如图所示,则下列式子正确的是( ).
A.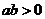
 B.
B.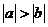 C.
C.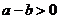 D.
D.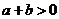
3.国家统计局统计资料显示,2005年第一季度我国国内生产总值为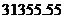 亿元,用科学记数法表示为( )元.(用四舍五入法保留3个有效数字)
亿元,用科学记数法表示为( )元.(用四舍五入法保留3个有效数字)
A.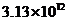 B.
B. 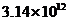
C. D.
D. 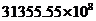
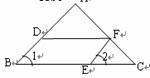
4.如图,在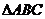 中,
中,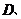
 分别在
分别在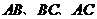 上,且
上,且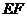 ∥
∥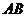 ,要使
,要使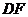 ∥
∥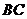 ,只需再有下列条件中的( )即可.
,只需再有下列条件中的( )即可.
A.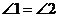 B.
B.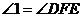 C.
C.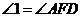 D.
D.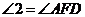
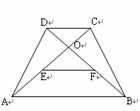
5.如图,等腰梯形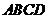 中,
中,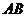 ∥
∥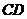 ,
,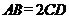 ,
,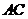 交
交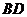 于点
于点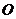 ,点
,点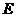 、
、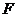 分别为
分别为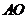 、
、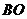 的中点,则下列关于点
的中点,则下列关于点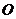 成中心对称的一组三角形是( ).
成中心对称的一组三角形是( ).
A.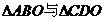 B.
B.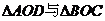
C.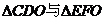 D.
D.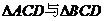
6.已知圆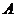 和圆
和圆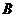 相切,两圆的圆心距为8cm,圆
相切,两圆的圆心距为8cm,圆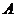 的半径为3cm,则圆
的半径为3cm,则圆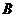 的半径是( ).
的半径是( ).
A.5cm B.11cm C.3cm D.5cm或11cm
7.某乡镇有甲、乙两家液化气站,他们的每罐液化气的价格、质和量都相同.为了促销,甲站的液化气每罐降价25%销售;每个用户购买乙站的液化气,第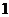 罐按照原价销售,若用户继续购买,则从第
罐按照原价销售,若用户继续购买,则从第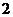 罐开始以7折优惠,促销活动都是一年.若小明家每年购买8罐液化气,则购买液化气最省钱的方法是( ).
罐开始以7折优惠,促销活动都是一年.若小明家每年购买8罐液化气,则购买液化气最省钱的方法是( ).
A.买甲站的 B.买乙站的
C.买两站的都可以 D.先买甲站的1罐,以后再买乙站的
8.若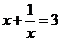 求
求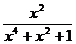 的值是( ).
的值是( ).
A.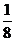 B.
B.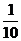 C.
C.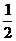 D.
D.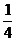
9.为了改善住房条件,小亮的父母考察了某小区的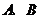 两套楼房,
两套楼房,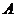 套楼房在第
套楼房在第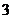 层楼,
层楼,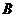 套楼房在第
套楼房在第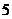 层楼,
层楼,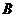 套楼房的面积比
套楼房的面积比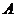 套楼房的面积大24平方米,两套楼房的房价相同,第3层楼和第5层楼的房价分别是平均价的1.1倍和0.9倍.为了计算两套楼房的面积,小亮设
套楼房的面积大24平方米,两套楼房的房价相同,第3层楼和第5层楼的房价分别是平均价的1.1倍和0.9倍.为了计算两套楼房的面积,小亮设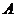 套楼房的面积为
套楼房的面积为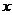 平方米,
平方米,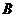 套楼房的面积为
套楼房的面积为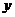 平方米,根据以上信息列出了下列方程组.其中正确的是( ).
平方米,根据以上信息列出了下列方程组.其中正确的是( ).
A.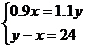 B.
B.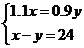
C.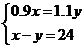 D.
D.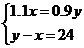
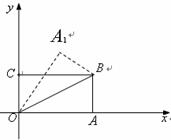
10.如图,在直角坐标系中,将矩形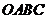 沿
沿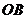 对折,使点
对折,使点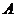 落在点
落在点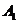 处,已知
处,已知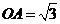 ,
,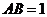 ,则点
,则点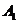 的坐标是( ).
的坐标是( ).
A.(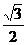 ,
,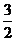 ) B.(
) B.(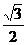 ,3)
,3)
C.(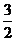 ,
,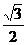 ) D.(
) D.(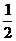 ,
,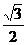 )
)
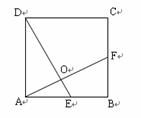
11.正方形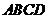 中,
中, 分别为
分别为 的中点,
的中点,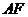 与
与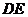 相交于点
相交于点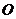 ,则
,则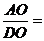 ( ).
( ).
A.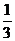 B.
B. C.
C.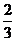 D.
D.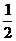
12.某种品牌的同一种洗衣粉有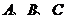 三种袋装包装,每袋分别装有400克、300克、200克洗衣粉,售价分别为
三种袋装包装,每袋分别装有400克、300克、200克洗衣粉,售价分别为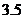 元、2.8元、1.9元.
元、2.8元、1.9元.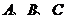 三种包装的洗衣粉每袋包装费用(含包装袋成本)分别为0.8元、0.6元、0.5元.厂家销售
三种包装的洗衣粉每袋包装费用(含包装袋成本)分别为0.8元、0.6元、0.5元.厂家销售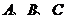 三种包装的洗衣粉各1200千克,获得利润最大的是( ).
三种包装的洗衣粉各1200千克,获得利润最大的是( ).
A.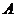 种包装的洗衣粉 B.
种包装的洗衣粉 B.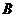 种包装的洗衣粉
种包装的洗衣粉
C.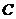 种包装的洗衣粉 D.三种包装的都相同
种包装的洗衣粉 D.三种包装的都相同
第Ⅱ卷
二、填空题(本大题共5小题,共15分.只要求填写最后结果,每小题填对得3分.其中,第14、15两小题为选做题,只须做 题中的一个即可,若两题都做,只以
题中的一个即可,若两题都做,只以 题计分.)
题计分.)
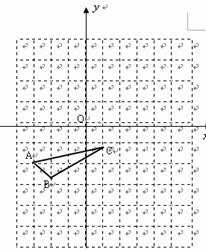
13.如图,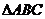 是格点(横、纵坐标都为整数的点)三角形,
是格点(横、纵坐标都为整数的点)三角形,
请在图中画出与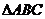 全等的一个格点三角形.
全等的一个格点三角形.
14.(A题) 已知一次函数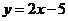 的图像与反比例函数
的图像与反比例函数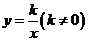 的图像交于第四象限的一点
的图像交于第四象限的一点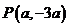 ,则这个反比例函数的解析式为_______________.
,则这个反比例函数的解析式为_______________.
(B题) 盒子里装有大小形状相同的3个白球和2个红球,搅匀后从中摸出一个球,放回搅匀后,再摸出第二个球,则取出的恰是两个红球的的概率是______.
15.(A题) 某电视台在每天晚上的黄金时段的3分钟内插播长度为20秒和40秒的两种广告,20秒广告每次收费6000元,40秒广告每次收费10000元.若要求每种广告播放不少于2次,且电视台选择收益最大的播放方式,则在这一天黄金时段3分钟内插播广告的最大收益是__元.
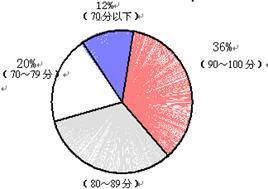
(B题) 一次数学测验以后,张老师根据某班成绩绘制了如图所示的扇形统计图(80~89分的百分比因故模糊不清),若80分以上(含80分)为优秀等级,则本次测验这个班的优秀率为_______.
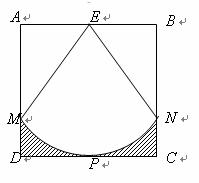
16.如图,正方形 的边长为
的边长为 ,点
,点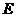 为
为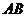 的中点,以
的中点,以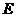 为圆心,1为半径作圆,分别交
为圆心,1为半径作圆,分别交 于
于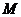
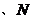 两点,与
两点,与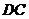 切于
切于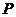 点.则图中阴影部分的面积是________.
点.则图中阴影部分的面积是________.
17在潍坊市“朝阳读书”系列活动中,某学校为活动优秀班级发放购书券到书店购买工具书.已知购买1本甲种书恰好用1张购书券,购买1本乙种或丙种书恰好都用2张购书券.某班用4张购书券购书,如果用完这4张购书券共有________________种不同购法(不考虑购书顺序).
三、解答题(本题共 小题,共
小题,共 分.解答应写出文字说明、证明过程或推演步骤.)
分.解答应写出文字说明、证明过程或推演步骤.)
18.(本题满分8分)
某年北京与巴黎的年降水量都是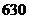 毫米,它们的月降水量占全年降水量百分比如下表:
毫米,它们的月降水量占全年降水量百分比如下表:
月 份
北 京
巴 黎
1
0.5%
6.7%
2
0.9%
5.8%
3
1.2%
6.7%
4
3.0%
7.8%
5
5.4%
8.8%
6
12.3%
9.4%
7
33.5%
9.4%
8
30.3%
9.0%
9
7.8%
9.0%
10
3.0%
9.9%
11
1.5%
9.0%
12
0.6%
8.5%
(1)计算两个城市的月平均降水量;
(2)写出两个城市的年降水量的众数和中位数;
(3)通过观察北京与巴黎两个城市的降水情况,用你所学的统计知识解释北京地区干旱与缺水的原因.
19.(本题满分8分)
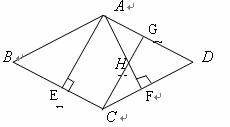
如图,菱形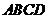 中,
中, ,
,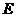 为
为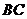 中点,
中点,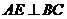 ,
,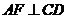 于点
于点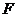 ,
,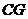 ∥
∥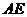 ,
,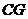 交
交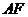 于点
于点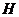 ,交
,交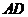 于点
于点 .
.
(1)求菱形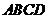 的面积;
的面积;
(2)求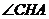 的度数.
的度数.
20.(本题满分9分)
为了加强学生的交通安全意识,某中学和交警大队联合举行了“我当一日小交警”活动,星期天选派部分学生到交通路口值勤,协助交通警察维护交通秩序.若每一个路口安排4人,那么还剩下78人;若每个路口安排8人,那么最后一个路口不足8人,但不少于4人.求这个中学共选派值勤学生多少人?共有多少个交通路口安排值勤?
21.(本题满分10分.从 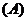 题、
题、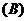 题中任选一题解答,若两题都答,只以
题中任选一题解答,若两题都答,只以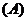 题计分)
题计分)
(A题)某市经济开发区建有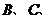
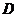 三个食品加工厂,这三个工厂和开发区
三个食品加工厂,这三个工厂和开发区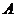 处的自来水厂正好在一个矩形的四个顶点上,它们之间有公路相通,且
处的自来水厂正好在一个矩形的四个顶点上,它们之间有公路相通,且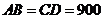 米,
米,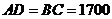 米.自来水公司已经修好一条自来水主管道
米.自来水公司已经修好一条自来水主管道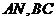 两厂之间的公路与自来水管道交于
两厂之间的公路与自来水管道交于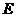 处,
处,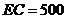 米.若自来水主管道到各工厂的自来水管道由各厂负担,每米造价800元.
米.若自来水主管道到各工厂的自来水管道由各厂负担,每米造价800元.
(1) 要使修建自来水管道的造价最低,这三个工厂的自来水管道路线应怎样设计?
并在图形中画出;
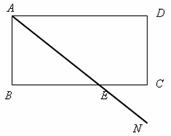
(2)求出各厂所修建的自来水管道的最低的造价各是多少元?
(B题)如图,已知平行四边形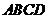 及四边形外一直线
及四边形外一直线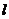 ,四个顶点
,四个顶点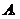
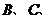
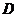 到直线
到直线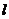 的距离分别为
的距离分别为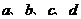 .
.
(1)观察图形,猜想得出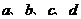 满足怎样的关系式?证明你的结论.
满足怎样的关系式?证明你的结论.
(2)现将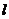 向上平移,你得到的结论还一定成立吗?请分情况写出你的结论.
向上平移,你得到的结论还一定成立吗?请分情况写出你的结论.
22.(本题满分10分)
某工厂生产的某种产品按质量分为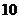 个档次,生产第一档次(即最低档次)的产品一天生产
个档次,生产第一档次(即最低档次)的产品一天生产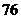 件,每件利润
件,每件利润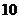 元,每提高一个档次,利润每件增加
元,每提高一个档次,利润每件增加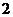 元.
元.
(1)每件利润为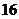 元时,此产品质量在第几档次?
元时,此产品质量在第几档次?
(2)由于生产工序不同,此产品每提高一个档次,一天产量减少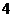 件.若生产第
件.若生产第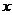 档的产品一天的总利润为
档的产品一天的总利润为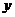 元(其中
元(其中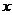 为正整数,且
为正整数,且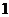 ≤
≤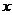 ≤
≤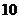 ),求出
),求出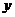 关于
关于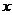 的函数关系式;若生产某档次产品一天的总利润为
的函数关系式;若生产某档次产品一天的总利润为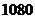 元,该工厂生产的是第几档次的产品?
元,该工厂生产的是第几档次的产品?
 . (本题满分
. (本题满分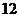 分)
分)
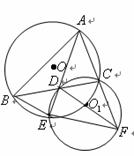
如图,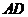 是
是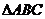 的角平分线, 延长
的角平分线, 延长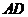 交
交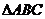 的外接圆
的外接圆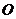 于点
于点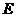 ,过
,过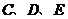 三点的圆
三点的圆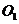 交
交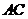 的延长线于点
的延长线于点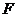 ,连结
,连结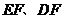 .
.
(1)求证: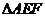 ∽
∽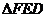 ;
;
(2) 若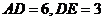 , 求
, 求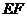 的长;
的长;
(3) 若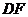 ∥
∥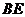 , 试判断
, 试判断 的形状,并说明理由.
的形状,并说明理由.
24.(本题满分12分)
抛物线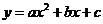 交
交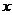 轴于
轴于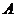 、
、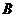 两点,交
两点,交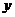 轴于点
轴于点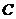 ,已知抛物线的对称轴为
,已知抛物线的对称轴为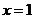 ,
,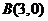 ,
,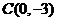 ,
,
(1)求二次函数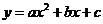 的解析式;
的解析式;
(2) 在抛物线对称轴上是否存在一点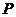 ,使点
,使点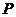 到
到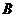 、
、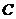 两点距离之差最大?若存在,求出
两点距离之差最大?若存在,求出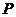 点坐标;若不存在,请说明理由;
点坐标;若不存在,请说明理由;
(3)平行于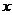 轴的一条直线交抛物线于
轴的一条直线交抛物线于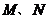 两点,若以
两点,若以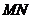 为直径的圆恰好与
为直径的圆恰好与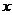 轴相切,求此圆的半径.
轴相切,求此圆的半径.