题目内容
【题目】某同学想研究滑块在倾斜气垫导轨上滑行时的加速度．如图1所示，他将导轨固定一定的倾角．在导轨B点固定一个光电门，让带有挡光片的滑块在不同位置由静止滑下．滑行时可以认为不受斜面阻力．把滑块到光电门的距离记为L．已知挡光片宽度为d．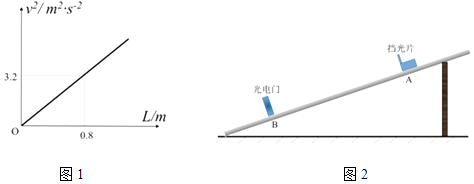
（1）为完成实验，需要记录什么数据？（用文字和符号共同表示）
（2）计算滑块加速度的表达式为a=（用符号表示）
（3）改变位置，重复实验，得到如图2所示的图象，则滑块的加速度大小a= ． （结果保留2位有效数字）
（4）为进一步研究滑块加速度a与导轨倾角θ的关系．该同学改变倾角的大小，在同一位置静止释放滑块，通过计算得到表格所示的数据．
根据表格数据可知实验结论为 ．
θ | 30° | 45° | 60° |
sinθ |
|
|
|
cosθ |
|
|
|
a（m/s2） | 5 | 5 | 5 |
【答案】
（1）滑块通过光电门所用的时间t
（2）
（3）2.0m/s2
（4）加速度与sinθ成正比,比例系数为10
【解析】解：（1）滑块经过光电门时的速度：v= 
，滑块做初速度为零的匀加速直线运动，由匀变速直线运动的速度位移公式得：v2=2aL，解得：a= 
= ，
已知：d、L，实验还需要测出：滑块通过光电门所用的时间t；（2）由（1）的分析可知，加速度：a= ；（3）由匀变速直线运动的速度位移公式得：v2=2aL，则：v2﹣L图象的斜率：k=2a= 
=4.0，加速度：a= 
= 
=2.0m/s2；（4）由表中实验数据可知，随倾角θ增大，加速度增大，且加速度与sinθ成正比， 
= 
=10，与cosθ既不成正比也不反比，由此可知：加速度与sinθ成正比，比例系数为10．
所以答案是：（1）滑块通过光电门所用的时间t；（2） ；（3）2.0m/s2；（4）加速度与sinθ成正比，比例系数为10．
【考点精析】关于本题考查的匀变速直线运动的速度、位移、时间的关系和加速度，需要了解速度公式：V=V0+at；位移公式：s=v0t+1/2at2；速度位移公式：vt2-v02=2as；以上各式均为矢量式，应用时应规定正方向，然后把矢量化为代数量求解，通常选初速度方向为正方向，凡是跟正方向一致的取“+”值，跟正方向相反的取“-”值；加速度与速度无关.只要速度在变化，无论速度大小，都有加速度;只要速度不变化（匀速），无论速度多大，加速度总是零;只要速度变化快，无论速度是大、是小或是零，物体加速度就大；方向与速度变化Δv的方向一致，但不一定与v的方向一致才能得出正确答案．
