Question

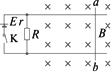
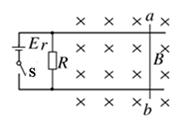
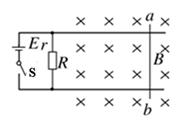
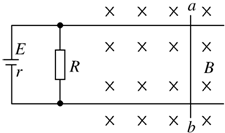轻直导线杆ab沿垂直于轨道方向放在水平平行的光滑轨道上，ab杆所在区域充满竖直向下的匀强磁场，如图所示，磁感应强度B=0.2T，轨道间距为10cm，当给ab杆施加一个大小为0.04N，方向水平向左的力时，ab杆恰好静止不动，已知电源内阻r=1Ω，电阻R=8Ω，ab杆电阻为4Ω，导轨电阻不计，求电源电动势．

Answer 1

分析：以杆为研究对象，受力分析，利用杆恰好静止列平衡方程，求出路段电压；再利用闭合电路的电压、电流关系和闭合电路的欧姆定律求解．

解答：解：设外电压为U，则通过杆的电流为I=

U

Rab

当杆静止时，F_安=F
即B

U

Rab

L=F，
  所以：U=

FRab

BL

=

0.04×4

0.2×0.1

 V=8 V．
通过电源的总电流
I=

U

R外

=

U

RRab R+Rab

=

8

8×4 8+4

 A=3 A．
由闭合电路的欧姆定律得：
E=U+Ir=8 V+3×1 V=11 V．
答：电源电动势为11 V．

点评：明确动力学和电学的联系纽带--安培力F=BIL，灵活应用平衡态和电路的知识求解，注意杆在电学中视为电阻．