题目内容
如图所示,在一条直线上两个振源A、B相距6m,振动频率相等,从t0时刻A、B开始振动,且都只振动一个周期,振幅相等,振动图像A为甲,B为乙。若A向右传播的波与B向左传播在t1 = 0.3s时相遇,则 ( )
A.两列波在A、B间的传播速度均为10m/s
B.两列波的波长都是4m
C.在两列波相遇过程中,中点C为振动加强点
D.t2 = 0.7s时刻B点经过平衡位置且振动方向向下

【答案】AD
【解析】由题意可知,波在t1 = 0.3s内传播的路程
s = 3m,可以由![]() 计算出波速v = 10m/s,故选项A正确;由图像可知T = 0.2s,根据公式
计算出波速v = 10m/s,故选项A正确;由图像可知T = 0.2s,根据公式![]() 可以计算出
可以计算出![]() = 2m,选项B错误;波由A传到C与由B传到C都是3m,即传播了1.5
= 2m,选项B错误;波由A传到C与由B传到C都是3m,即传播了1.5![]() ,又因为A、B两个振源是反相的,故C为振动减弱点,选项C错误;由于B点自身只振动一个周期,即自身振动时间为0.2s,此后B点的振动则是由于A点产生的波传播到B点引起的,分析可知在0.6s时刻,A波的波前到达B点;在t2 = 0.7s时刻,B点由于A波的传播已做了0.5T的振动,此时B质点经过平衡位置,其振动方向向下,故选项D正确.
,又因为A、B两个振源是反相的,故C为振动减弱点,选项C错误;由于B点自身只振动一个周期,即自身振动时间为0.2s,此后B点的振动则是由于A点产生的波传播到B点引起的,分析可知在0.6s时刻,A波的波前到达B点;在t2 = 0.7s时刻,B点由于A波的传播已做了0.5T的振动,此时B质点经过平衡位置,其振动方向向下,故选项D正确.
【点评】波传播的本质是波形的平移,当两列波相遇时,满足波的叠加原理。

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
 如图所示,在一条直线上有两个相距0.4m的点电荷A、B,A带电+Q,B带电-9Q.现引入第三个点电荷C,恰好使三个点电荷均在电场力的作用下处于平衡状态,问:C应带什么性质的电?应放于何处?所带电荷量为多少?
如图所示,在一条直线上有两个相距0.4m的点电荷A、B,A带电+Q,B带电-9Q.现引入第三个点电荷C,恰好使三个点电荷均在电场力的作用下处于平衡状态,问:C应带什么性质的电?应放于何处?所带电荷量为多少? 如图所示,在一条直线上两个振源A、B相距6m,振动频率相等,从t0=0时刻A、B开始振动,且都只振动一个周期,振幅相等,A、B振动图象分别为甲、乙,若A向右传播的波与B向左传播的波在t1=0.3s时相遇,则( )
如图所示,在一条直线上两个振源A、B相距6m,振动频率相等,从t0=0时刻A、B开始振动,且都只振动一个周期,振幅相等,A、B振动图象分别为甲、乙,若A向右传播的波与B向左传播的波在t1=0.3s时相遇,则( )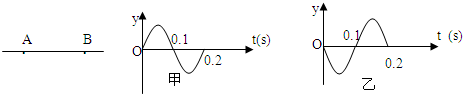
 (2006?红桥区模拟)如图所示,在一条直线上两个振动源A、B相距6m,振动频率相等,t0=0时刻A、B开始振动,且都只振动一个周期,振幅相等,A振动图象如图甲所示,B振动图象如图乙所示,若A向右传播的波与B向左传播的波在t1=0.3s时相遇.则
(2006?红桥区模拟)如图所示,在一条直线上两个振动源A、B相距6m,振动频率相等,t0=0时刻A、B开始振动,且都只振动一个周期,振幅相等,A振动图象如图甲所示,B振动图象如图乙所示,若A向右传播的波与B向左传播的波在t1=0.3s时相遇.则