Question

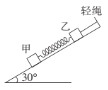
【题目】如图所示，在倾角为30°的光滑斜面上，甲、乙两物体通过轻弹簧连接，乙物体通过轻绳与斜面顶端相连。已知甲的质量是乙质量的2倍，轻弹簧、轻绳均与斜面平行，重力加速度大小为g。现剪断轻绳，设剪断轻绳的瞬间甲和乙的加速度大小分别为、，则有（ ）

A.B.

C.D.

Answer 1

【答案】C

【解析】

对甲在剪断绳子之前，甲处于平衡状态，所以弹簧的拉力等于甲的重力沿斜面的分力相等；在剪断上端的绳子的瞬间，绳子上的拉力立即减为零，而弹簧的伸长量没有来得及发生改变，故弹力不变仍为甲的重力沿斜面上的分力，故甲的加速度为零；

对乙在剪断绳子之前，乙也处于平衡状态，在沿斜面方向上绳子的拉力等于乙受到重力沿斜面的分力与弹簧对它斜向下的拉力的和，即

在剪断上端的绳子的瞬间，绳子上的拉力立即减为零，所以根据牛顿第二定律得

故C正确，ABD错误。

故选C。