题目内容
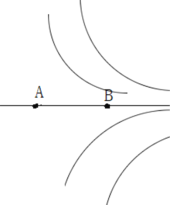
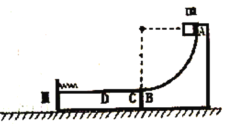
【题目】如图所示,半径R=2m的四分之一圆弧轨道AB固定在水平面上,左端固定有轻弹簧的长木板放置在光滑水平面上,紧靠圆弧轨道末端且上表面与轨道末端平齐,木板右侧CD段粗糙,左侧光滑。质量m=2kg的小滑块从轨道A端静止释放,滑块运动到圆弧轨道末端B点时对轨道的压力F=56N。已知长木板质量M=2kg,滑块与长木板CD段动摩擦因数![]() ,CD段长度L=1m,滑块可看作质点,弹簧自然伸长时右端没有到达D点,g取10m/s2。求:
,CD段长度L=1m,滑块可看作质点,弹簧自然伸长时右端没有到达D点,g取10m/s2。求:
(i)运动过程中系统弹性势能的最大值;
(ii)通过计算判断滑块最终是否会从长木板上滑落?
【答案】(ⅰ)8J (ⅱ)不会从木板上掉下来
【解析】
(ⅰ)滑块运动到B端时,由牛顿第二定律得:
![]()
解得
v=6m/s
滑块在木板上滑行过程,系统的动量守恒,设弹簧压缩到最短时系统速度为![]()
由动量守恒定律得:
![]()
解得
![]()
滑块滑过CD段,由于摩擦产生的热量
![]()
系统共速时动能
![]()
故最大弹性势能
![]()
(ⅱ)设木板足够长,有动量守恒定律得
![]()
得
v2=v1=3m/s
由能量守恒定律得:
![]()
解得
![]()
故弹簧将物块弹出后滑不出摩擦区CD,滑块不会从木板上掉下来.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目